题目内容
求垂直于直线x+3y-5=0，且与点P（-1，0）的距离是
的直线的方程．
| 3 |
| 5 |
| 10 |
∵直线x+3y-5=0的斜率为-
，
∴垂直于直线x+3y-5=0的直线的斜率为3，
则垂直于直线x+3y-5=0的直线方程可设为y=3x+m，即3x-y+m=0．
由点到直线的距离公式得，点P（-1，0）到3x-y+m=0的距离d=
=
，
解得：m=-3或m=9．
∴所求直线方程为：3x-y-3=0或3x-y+9=0．
| 1 |
| 3 |
∴垂直于直线x+3y-5=0的直线的斜率为3，
则垂直于直线x+3y-5=0的直线方程可设为y=3x+m，即3x-y+m=0．
由点到直线的距离公式得，点P（-1，0）到3x-y+m=0的距离d=
| |-1×3+m| | ||
|
| 3 |
| 5 |
| 10 |
解得：m=-3或m=9．
∴所求直线方程为：3x-y-3=0或3x-y+9=0．
练习册系列答案
相关题目
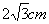
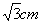
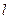经过点A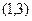
，求：（1）直线
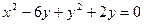关于直线OA对称的圆的方程。