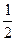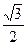题目内容
设直线y=2x+b与抛物线y2=4x相交于A,B两点,且|AB|=3
(1)求b值;
(2)设P(x0,0)是x轴上一点,当△PAB面积等于9时,求P点坐标.
| 5 |
(1)求b值;
(2)设P(x0,0)是x轴上一点,当△PAB面积等于9时,求P点坐标.
(1)由
,消去y得4x2+4(b-1)x+b2=0.
△=[4(b-1)]2-4×4×b2>0,得b<
.
x1+x2=1-b,x1•x2=
.
|AB|=
=
=3
.
∴解得:b=-4,满足b<
,∴b=-4;
(2)P到直线2x-y-4=0的距离为d,d=
.
由S△PAB=
×3
×
=9,解得:x=5或x=-1,
∴P点坐标为(-1,0)或(5,0).
|
△=[4(b-1)]2-4×4×b2>0,得b<
| 1 |
| 2 |
x1+x2=1-b,x1•x2=
| b2 |
| 4 |
|AB|=
| (1+22)[(x1+x2)2-4x1x2] |
| 5 |
| (1-b)2-b2 |
| 5 |
∴解得:b=-4,满足b<
| 1 |
| 2 |
(2)P到直线2x-y-4=0的距离为d,d=
| |2x0-4| | ||
|
由S△PAB=
| 1 |
| 2 |
| 5 |
| |2x0-4| | ||
|
∴P点坐标为(-1,0)或(5,0).

练习册系列答案
相关题目
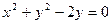 ,直线
,直线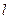 的倾斜角为
的倾斜角为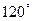 ,与圆M交于P、Q两点,若
,与圆M交于P、Q两点,若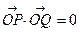 (O为原点),则
(O为原点),则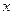 轴上的截距为 .
轴上的截距为 .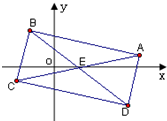
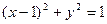 的圆心到直线
的圆心到直线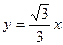 的距离是( )
的距离是( )