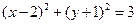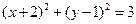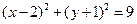题目内容
已知直线l:X-y+1=0,⊙O:x2+y2=2上的任意一点P到直线l的距离为d.当d取得最大时对应P的坐标(m,n),设g(x)=mx+
-2lnx.
(1)求证:当x≥1,g(x)≥0恒成立;
(2)讨论关于x的方程:mx+
-g(x)=2x3-4ex2+tx根的个数.
| n |
| x |
(1)求证:当x≥1,g(x)≥0恒成立;
(2)讨论关于x的方程:mx+
| n |
| x |
(1)由题意得P(1,-1),
∴m=1,n=-1∴g(x)=mx+
-2lnx=x-
-2lnx
∴g′(x)=1+
-
=
=
≥0,
∴g(x)在[1,+∞)是单调增函数,
∴g(x)≥g(1)=1-1-2ln1=0对于x∈[1,+∞)恒成立.
(2)方程mx+
-g(x)=2x3-4ex2+tx;
∴2lnx=2x3-4ex2+tx
∵x>0,∴方程为
=2x2-4ex+t
令L(x)=
,H(x)=2x2-4ex+t,
∵L′(x)=2
,当x∈(0,e)时,L′(x)≥0,
∴L′(x)在(0,e]上为增函数;x∈[e,+∞)时,L′(x)≤0,
∴L′(x)在[0,e)上为减函数,
当x=e时,L(x)max=L(e)=
H(x)=2x2-4ex+t=2(x-e)2+t-2e2,
∴可以分析①当t-2e2>
,即t>2e2+
时,方程无解.
②当t-2e2=
,即t=2e2+
时,方程有一个根.
③当t-2e2<
,即t<2e2+
时,方程有两个根.
∴m=1,n=-1∴g(x)=mx+
| n |
| x |
| 1 |
| x |
∴g′(x)=1+
| 1 |
| x2 |
| 2 |
| x |
| x2-2x+1 |
| x2 |
| (x-1)2 |
| x2 |
∴g(x)在[1,+∞)是单调增函数,
∴g(x)≥g(1)=1-1-2ln1=0对于x∈[1,+∞)恒成立.
(2)方程mx+
| n |
| x |
∴2lnx=2x3-4ex2+tx
∵x>0,∴方程为
| 2lnx |
| x |
令L(x)=
| 2lnx |
| x |
∵L′(x)=2
| 1-lnx |
| x2 |
∴L′(x)在(0,e]上为增函数;x∈[e,+∞)时,L′(x)≤0,
∴L′(x)在[0,e)上为减函数,
当x=e时,L(x)max=L(e)=
| 2 |
| e |
H(x)=2x2-4ex+t=2(x-e)2+t-2e2,
∴可以分析①当t-2e2>
| 2 |
| e |
| 2 |
| e |
②当t-2e2=
| 2 |
| e |
| 2 |
| e |
③当t-2e2<
| 2 |
| e |
| 2 |
| e |

练习册系列答案
相关题目
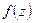 对一切实数
对一切实数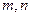 都有
都有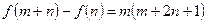 成立,且
成立,且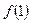 =0,
=0,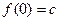 .曲线
.曲线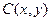 的参数方程是
的参数方程是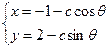 (
(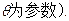 (1)求实数
(1)求实数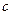 的值和曲线
的值和曲线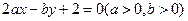 被曲线
被曲线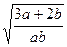 的最小值.
的最小值.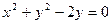 ,直线
,直线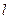 的倾斜角为
的倾斜角为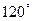 ,与圆M交于P、Q两点,若
,与圆M交于P、Q两点,若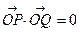 (O为原点),则
(O为原点),则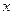 轴上的截距为 .
轴上的截距为 .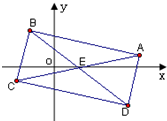
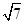 的⊙O中,弦AB,CD相交于点P. PA=PB=2,PD=1,则圆心O到弦CD的距离为________.
的⊙O中,弦AB,CD相交于点P. PA=PB=2,PD=1,则圆心O到弦CD的距离为________.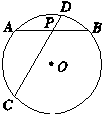
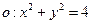 的两条相互垂直的弦,垂足为
的两条相互垂直的弦,垂足为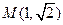 ,则四边形ABCD的面积的最大值为 .
,则四边形ABCD的面积的最大值为 .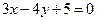 相切的圆的方程为
相切的圆的方程为