题目内容
20．不等式x2-4|x|+3＞0的解为（ ）| A． | x＜1或x＞3 | B． | x＜-3或x＞-1 | ||
| C． | x＜-3或-1＜x＜1或x＞3 | D． | 0≤x＜1或x＞3 |
分析 把不等式x2-4|x|+3＞0化为|x|2-4|x|+3＞0，求出含有绝对值的不等式的解即可．
解答 解：不等式x2-4|x|+3＞0可化为：
|x|2-4|x|+3＞0，
即（|x|-1）（|x|-3）＞0，
解得|x|＜1或|x|＞3；
∴-1＜x＜1，或x＜-3，或x＞3；
∴原不等式的解为{x|x＜-3或-1＜x＜1或x＞3}．
故选：C．
点评 本题考查了含有绝对值的不等式的解法与应用问题，是基础题目．
练习册系列答案
单元加期末复习先锋大考卷系列答案
出彩同步大试卷系列答案
相关题目
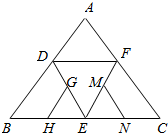如图是正四面体的平面展开图，G、H、M、N分别为DE、BE、EF、EC的中点，在这个正四面体中，