题目内容
12.当a$\frac{17}{16}$时,两曲线x=-y2+$\frac{5}{4}$和y=-x2+a(a>0)有切点.分析 根据题意,曲线可化为y1=f(x)=$\sqrt{\frac{5}{4}-x}$,y2=g(x)=-x2+a(a>0),则f′(x)=-$\frac{1}{2}$•$(\frac{5}{4}-x)^{-\frac{1}{2}}$,g′(x)=-2x,设切点(m,n),则f(m)=g(m),f′(m)=g′(m),即可得出结论.
解答 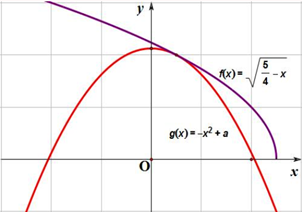 解:根据题意,曲线可化为y1=f(x)=$\sqrt{\frac{5}{4}-x}$,y2=g(x)=-x2+a(a>0),则
解:根据题意,曲线可化为y1=f(x)=$\sqrt{\frac{5}{4}-x}$,y2=g(x)=-x2+a(a>0),则
f′(x)=-$\frac{1}{2}$•$(\frac{5}{4}-x)^{-\frac{1}{2}}$,g′(x)=-2x,
设切点(m,n),则f(m)=g(m),f′(m)=g′(m),
解得m=1,n=$\frac{1}{4}$,a=$\frac{17}{16}$,
∴a=$\frac{17}{16}$,两曲线x=-y2+$\frac{5}{4}$和y=-x2+a(a>0)有切点.
故答案为:$\frac{17}{16}$.
点评 本题考查导数知识的综合运用,考查导数的几何意义,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.不等式x2-4|x|+3>0的解为( )
| A. | x<1或x>3 | B. | x<-3或x>-1 | ||
| C. | x<-3或-1<x<1或x>3 | D. | 0≤x<1或x>3 |
1.要使式子$\sqrt{\frac{x-2}{x+2}}$有意义,则x的取值范围是( )
| A. | x∈(-∞,-2)∪[2,+∞) | B. | x∈(-∞,-2]∪[2,+∞) | C. | x∈(-2,2) | D. | x∈[-2,2] |
 浑南“万达广场”五一期间举办“万达杯”游戏大赛.每5人组成一队,编号为1,2,3,4,5,在其中的投掷飞镖比赛中,要求随机抽取3名队员参加,每人投掷一次.假设飞镖每次都能投中靶面,且靶面上每点被投中的可能性相同.某人投中靶面内阴影区域记为“成功”(靶面为圆形,ABCD为正方形).每队至少有2人“成功”则可获得奖品(其中任何两位队员“成功”与否互不影响).
浑南“万达广场”五一期间举办“万达杯”游戏大赛.每5人组成一队,编号为1,2,3,4,5,在其中的投掷飞镖比赛中,要求随机抽取3名队员参加,每人投掷一次.假设飞镖每次都能投中靶面,且靶面上每点被投中的可能性相同.某人投中靶面内阴影区域记为“成功”(靶面为圆形,ABCD为正方形).每队至少有2人“成功”则可获得奖品(其中任何两位队员“成功”与否互不影响). 如图所示是三棱锥D-ABC的三视图,若在三棱锥的直观图中,点O为线段BC的中点,则异面直线DO与AB所成角的余弦值等于$\frac{\sqrt{6}}{6}$.
如图所示是三棱锥D-ABC的三视图,若在三棱锥的直观图中,点O为线段BC的中点,则异面直线DO与AB所成角的余弦值等于$\frac{\sqrt{6}}{6}$.