题目内容
8.已知a∈R,函数f(x)=x|x-a|,(Ⅰ)当a=2时,作出图形并写出函数y=f(x)的单调递增区间;
(Ⅱ)当a=-2时,求函数y=f(x)在区间$(-\sqrt{2}-1,2]$的值域;
(Ⅲ)设a>0,函数f(x)在(m,n)上既有最大值又有最小值,请分别求出m、n的取值范围(用a表示).
分析 (Ⅰ)当a=2时,化简函数解析式,作出图形并写出函数y=f(x)的单调递增区间.
(Ⅱ)利用函数的图象判断函数在(-2,-1)是减函数,在(-1,2)是减函数,求出函数的最值.
(Ⅲ)化简函数$f(x)=\left\{\begin{array}{l}x(x-a),x≥a\\ x(a-x),x<a\end{array}\right.$,画出图象,利用最值,求解范围即可.
解答 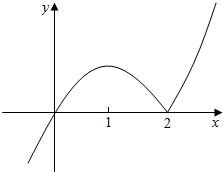 (Ⅰ)解:当a=2时,f(x)=x|x-2|=$\left\{\begin{array}{l}x(x-2),x≥2\\ x(2-x),x<2\end{array}\right.$,作出图象 …(2分)
(Ⅰ)解:当a=2时,f(x)=x|x-2|=$\left\{\begin{array}{l}x(x-2),x≥2\\ x(2-x),x<2\end{array}\right.$,作出图象 …(2分)
由图象可知,
单调递增区间为(-∞,1],[2,+∞)…(4分)
(Ⅱ)∵$f(x)在(-\sqrt{2}-1,-2)$是增函数,在(-2,-1)是减函数,在(-1,2)是减函数,…(6分)
∴f(x)min=f(-1)=-1∴f(x)max=8…(8分)
∴f(x)的值域为[-1,8]…(10分)
(Ⅲ)$f(x)=\left\{\begin{array}{l}x(x-a),x≥a\\ x(a-x),x<a\end{array}\right.$
当a>0时,图象如图所示
由$\left\{\begin{array}{l}y=\frac{a^2}{4}\\ y=x(x-a)\end{array}\right.$得$x=\frac{{(\sqrt{2}+1)a}}{2}$…(12分)
∴$0≤m<\frac{a}{2}$,$a<n≤\frac{{\sqrt{2}+1}}{2}a$…(16分)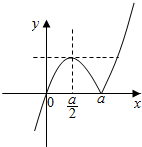
点评 本题考查函数的解析式的化简,图象的作法,函数的最值的解法,考查转化思想以及计算能力.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
18.若$\overrightarrow{a}$=(2,3),$\overrightarrow{b}$=(-4,7),则$\overrightarrow{a}$在$\overrightarrow{b}$上的投影为( )
| A. | $\sqrt{13}$ | B. | $\frac{{\sqrt{65}}}{5}$ | C. | 13 | D. | $\sqrt{65}$ |
19.不等式|3x-4|≤5的解集是( )
| A. | {x|-$\frac{1}{3}$<x<3} | B. | {x|x≤-$\frac{1}{3}$或x≥3} | C. | {x|$\frac{1}{3}$≤x≤-3} | D. | {x|-$\frac{1}{3}$≤x≤3} |
20.设等差数列{an}的前n项和为Sn,若$\frac{{S}_{3}}{{S}_{6}}$=$\frac{1}{3}$,则$\frac{S_6}{{{S_{12}}}}$的值为( )
| A. | $\frac{10}{3}$ | B. | $\frac{3}{10}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{4}$ |
18.已知sinα=-$\frac{{\sqrt{3}}}{3}$,且α是第三象限角,则sin2α-tanα=( )
| A. | $\frac{{\sqrt{2}}}{3}$ | B. | $\frac{{\sqrt{2}}}{4}$ | C. | $\frac{{\sqrt{2}}}{6}$ | D. | $\frac{{\sqrt{2}}}{8}$ |