题目内容
18.已知sinα=-$\frac{{\sqrt{3}}}{3}$,且α是第三象限角,则sin2α-tanα=( )| A. | $\frac{{\sqrt{2}}}{3}$ | B. | $\frac{{\sqrt{2}}}{4}$ | C. | $\frac{{\sqrt{2}}}{6}$ | D. | $\frac{{\sqrt{2}}}{8}$ |
分析 由sinα及α为第三象限角,利用同角三角函数间的基本关系求出cosα的值,进而求出tanα的值,原式变形后代入计算即可求出值.
解答 解:∵sinα=-$\frac{{\sqrt{3}}}{3}$,且α是第三象限角,
∴cosα=-$\sqrt{1-si{n}^{2}α}$=-$\frac{\sqrt{6}}{3}$,tanα=$\frac{\sqrt{2}}{2}$,
则原式=2sinαcosα-tanα=2×(-$\frac{\sqrt{3}}{3}$)×(-$\frac{\sqrt{6}}{3}$)-$\frac{\sqrt{2}}{2}$=$\frac{\sqrt{2}}{6}$,
故选:C.
点评 此题考查了同角三角函数间基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
9.首项为-4的等差数列{an}从第10项起为正数,则公差d的取值范围为( )
| A. | $({\frac{4}{9},+∞})$ | B. | $({\frac{4}{9},\frac{1}{2}})$ | C. | $({\frac{4}{9},\frac{1}{2}}]$ | D. | $({-∞,\frac{4}{9}})$ |
13.已知点An(n,an)(n∈N*)都在函数y=ax(a>0,a≠1)的图象上,则a4+a6与2a5的大小关系是( )
| A. | a4+a6>2a5 | B. | a4+a6<2a5 | ||
| C. | a4+a6=2a5 | D. | a4+a6与2a5的大小与a有关 |
10.已知函数f(x)=$\frac{{e}^{x}+m}{{e}^{x}+1}$,若对?a,b,c∈R,都有f(a)+f(b)>f(c)成立,则实数m的取值范围是[$\frac{1}{2}$,2].
7.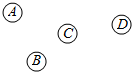 如图,A、B、C、D为四个村庄,要修筑三条公路,将这四个村庄连起来,则不同的修筑方法共有( )
如图,A、B、C、D为四个村庄,要修筑三条公路,将这四个村庄连起来,则不同的修筑方法共有( )
 如图,A、B、C、D为四个村庄,要修筑三条公路,将这四个村庄连起来,则不同的修筑方法共有( )
如图,A、B、C、D为四个村庄,要修筑三条公路,将这四个村庄连起来,则不同的修筑方法共有( )| A. | 8种 | B. | 12种 | C. | 16种 | D. | 20种 |
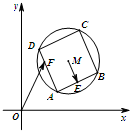 如图,已知圆M:(x-3)2+(y-3)2=4,四边形ABCD为圆M的内接正方形,E为边AB的中点,当正方形ABCD绕圆心M转动,同时点F在边AD上运动时,$\overrightarrow{ME}$$•\overrightarrow{OF}$的最大值是8.
如图,已知圆M:(x-3)2+(y-3)2=4,四边形ABCD为圆M的内接正方形,E为边AB的中点,当正方形ABCD绕圆心M转动,同时点F在边AD上运动时,$\overrightarrow{ME}$$•\overrightarrow{OF}$的最大值是8.