题目内容
19.不等式|3x-4|≤5的解集是( )| A. | {x|-$\frac{1}{3}$<x<3} | B. | {x|x≤-$\frac{1}{3}$或x≥3} | C. | {x|$\frac{1}{3}$≤x≤-3} | D. | {x|-$\frac{1}{3}$≤x≤3} |
分析 由不等式可得可得-5≤3x-4≤5,由此求得x的范围.
解答 解:由不等式|3x-4|≤5,可得-5≤3x-4≤5,求得-$\frac{1}{3}$≤x≤3,
故选:D.
点评 本题主要考查分式不等式的解法,体现了等价转化的数学思想,属于基础题.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
9.${(\root{3}{x}+\frac{1}{x})^n}$的展开式中第5项是常数项,那么这个展开式中系数最大的项为( )
| A. | 第9项 | B. | 第8项 | C. | 第9项和第10项 | D. | 第8项和第9项 |
7.阅读程序框图,任意输入一次x(-1≤x≤1)与y(-1≤y≤1),则能输出数对(x,y)的概率为( )
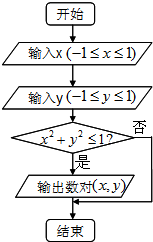

| A. | $\frac{1}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{4}$ |
9.首项为-4的等差数列{an}从第10项起为正数,则公差d的取值范围为( )
| A. | $({\frac{4}{9},+∞})$ | B. | $({\frac{4}{9},\frac{1}{2}})$ | C. | $({\frac{4}{9},\frac{1}{2}}]$ | D. | $({-∞,\frac{4}{9}})$ |
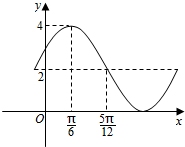 已知函数y=Asin(ωx+φ)+B的一部分图象如图所示,如果A>0,ω>0,|φ|<$\frac{π}{2}$,则其解析式为y=2sin(2x+$\frac{π}{6}$)+2..
已知函数y=Asin(ωx+φ)+B的一部分图象如图所示,如果A>0,ω>0,|φ|<$\frac{π}{2}$,则其解析式为y=2sin(2x+$\frac{π}{6}$)+2..