题目内容
20.设等差数列{an}的前n项和为Sn,若$\frac{{S}_{3}}{{S}_{6}}$=$\frac{1}{3}$,则$\frac{S_6}{{{S_{12}}}}$的值为( )| A. | $\frac{10}{3}$ | B. | $\frac{3}{10}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{4}$ |
分析 通过等差数列的性质可得S3、S6-S3、S9-S6、S12-S9成等差数列,利用$\frac{{S}_{3}}{{S}_{6}}$=$\frac{1}{3}$计算即得结论.
解答 解:∵等差数列{an}的前n项和为Sn,
∴S3、S6-S3、S9-S6、S12-S9成等差数列,
又∵$\frac{{S}_{3}}{{S}_{6}}$=$\frac{1}{3}$,
∴S6=3S3,
∴(S6-S3)-S3=S3,
S9-S6=(S6-S3)+S3=S6=3S3,
S12-S9=(S9-S6)+S3=4S3,
∴(S12-S9)+(S9-S6)=S12-S6=7S3,
∴S12=S6+7S3=3S3+7S3=10S3,
∴$\frac{S_6}{{{S_{12}}}}$=$\frac{3{S}_{3}}{10{S}_{3}}$=$\frac{3}{10}$,
故选:B.
点评 本题考查等差数列的性质,注意解题方法的积累,属于中档题.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
5.命题:?x∈[0,$\frac{π}{2}$],sinx+cosx≥2的否定是( )
| A. | ?x∈[0,$\frac{π}{2}$],sinx+cosx<2 | B. | ?x∈[0,$\frac{π}{2}$],sinx+cosx≥2 | ||
| C. | ?x∈[0,$\frac{π}{2}$],sinx+cosx≤2 | D. | ?x∈[0,$\frac{π}{2}$],sinx+cosx<2 |
12.已知点A(-1,-1)和向量$\overrightarrow a$=(2,3),若$\overrightarrow{AB}$=3$\overrightarrow a$,则点B的坐标是(5,8).
9.首项为-4的等差数列{an}从第10项起为正数,则公差d的取值范围为( )
| A. | $({\frac{4}{9},+∞})$ | B. | $({\frac{4}{9},\frac{1}{2}})$ | C. | $({\frac{4}{9},\frac{1}{2}}]$ | D. | $({-∞,\frac{4}{9}})$ |
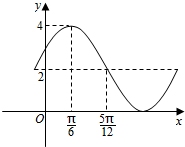 已知函数y=Asin(ωx+φ)+B的一部分图象如图所示,如果A>0,ω>0,|φ|<$\frac{π}{2}$,则其解析式为y=2sin(2x+$\frac{π}{6}$)+2..
已知函数y=Asin(ωx+φ)+B的一部分图象如图所示,如果A>0,ω>0,|φ|<$\frac{π}{2}$,则其解析式为y=2sin(2x+$\frac{π}{6}$)+2..