题目内容
16.已知向量$\overrightarrow{m}$=(sin2x,-$\frac{\sqrt{3}}{2}$),$\overrightarrow{n}$=($\frac{1}{2}$,cos2x),函数f(x)=$\overrightarrow{m}$•$\overrightarrow{n}$.(Ⅰ)试用五点作图法画出函数f(x)在一个周期内的图象(要求列表);
(Ⅱ)求方程f(x)=m(0<m<1)在[-$\frac{π}{12}$,$\frac{35π}{12}$]内的所有实数根之和.
分析 (Ⅰ)利用向量的数量积求出f(x)的表达式,然后利用五点作图法画出函数f(x)在一个周期内的图象;
(Ⅱ)利用函数f(x)=m在[-$\frac{π}{12}$,$\frac{35π}{12}$]内对称性,求出相应的对称轴,进行求解即可.
解答 解:(Ⅰ)f(x)=$\overrightarrow{m}$•$\overrightarrow{n}$=$\frac{1}{2}$sin2x-$\frac{\sqrt{3}}{2}$cos2x=sin(2x-$\frac{π}{3}$),…(2分)
列对应值表如下:
| 2x-$\frac{π}{3}$ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | $\frac{π}{6}$ | $\frac{5π}{12}$ | $\frac{2π}{3}$ | $\frac{11π}{12}$ | $\frac{7π}{6}$ |
| f(x) | 0 | 1 | 0 | -1 | 0 |
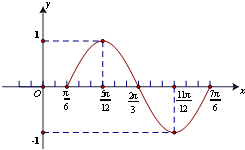 …(4分)
…(4分)通过描出五个关键点,再用光滑曲线顺次连接作出函数f(x)在一个周期内的图象如下图所示:
…(6分)
(Ⅱ)∵y=sin(2x-$\frac{π}{3}$)的周期t=π,
∴y=sin(2x-$\frac{π}{3}$)在[-$\frac{π}{12}$,$\frac{35π}{12}$]内有3个周期. …(7分)
令2x-$\frac{π}{3}$=kπ+$\frac{π}{2}$,k∈Z,
∴x=$\frac{5π}{12}$+$\frac{kπ}{2}$,k∈Z,
即函数y=sin(2x-$\frac{π}{3}$)的对称轴为x=$\frac{5π}{12}$+$\frac{kπ}{2}$,k∈Z.…(8分)
又x∈[-$\frac{π}{12}$,$\frac{35π}{12}$],则2x-$\frac{π}{3}$∈[-$\frac{π}{2}$,$\frac{11π}{2}$],且0<m<1,
∴f(x)=m(0<m<1)在[-$\frac{π}{12}$,$\frac{35π}{12}$]内有6个实根,…(9分)
不妨从小到大依次设为xi,(i=1,2,3,4,5,6),
则$\frac{{x}_{1}+{x}_{2}}{2}=\frac{5π}{12}$,$\frac{{x}_{3}+{x}_{4}}{2}$=$\frac{17π}{12}$,$\frac{{x}_{5}+{x}_{6}}{2}$=$\frac{29π}{12}$
即x1+x2=$\frac{5π}{6}$,x3+x4=$\frac{17π}{6}$,x5+x6=$\frac{29π}{6}$,
∴所有实数根之和=x1+x2+x3+x4+x5+x6=$\frac{5π}{6}$+$\frac{17π}{6}$+$\frac{29π}{6}$=$\frac{17π}{2}$.…(12分)
点评 本题主要考查三角函数的图象做法,要掌握五点法作图,同时利用三角函数的对称性是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.阅读程序框图,任意输入一次x(-1≤x≤1)与y(-1≤y≤1),则能输出数对(x,y)的概率为( )
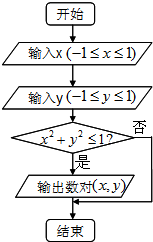

| A. | $\frac{1}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{4}$ |
1.给出的下列函数中在$(\frac{π}{2},π)$上是增函数的是( )
| A. | y=sinx | B. | y=cosx | C. | y=sin2x | D. | y=cos2x |
5.命题:?x∈[0,$\frac{π}{2}$],sinx+cosx≥2的否定是( )
| A. | ?x∈[0,$\frac{π}{2}$],sinx+cosx<2 | B. | ?x∈[0,$\frac{π}{2}$],sinx+cosx≥2 | ||
| C. | ?x∈[0,$\frac{π}{2}$],sinx+cosx≤2 | D. | ?x∈[0,$\frac{π}{2}$],sinx+cosx<2 |