题目内容
17.△ABC的内角A,B,C所对边的长分别是a,b,c,若$C=\frac{π}{3},a=1,b=2$,则c=$\sqrt{3}$.分析 由余弦定理c2=a2+b2-2abcosC,代入数据,即可得解.
解答 解:由余弦定理c2=a2+b2-2abcosC=1+4-2×$1×2×cos\frac{π}{3}$=3,
解得c=$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 本题考查余弦定理的运用,考查运算能力,属于基础题.

练习册系列答案
相关题目
7.阅读程序框图,任意输入一次x(-1≤x≤1)与y(-1≤y≤1),则能输出数对(x,y)的概率为( )
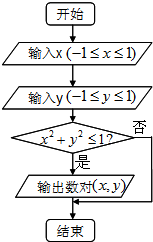

| A. | $\frac{1}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{4}$ |
5.命题:?x∈[0,$\frac{π}{2}$],sinx+cosx≥2的否定是( )
| A. | ?x∈[0,$\frac{π}{2}$],sinx+cosx<2 | B. | ?x∈[0,$\frac{π}{2}$],sinx+cosx≥2 | ||
| C. | ?x∈[0,$\frac{π}{2}$],sinx+cosx≤2 | D. | ?x∈[0,$\frac{π}{2}$],sinx+cosx<2 |
12.已知点A(-1,-1)和向量$\overrightarrow a$=(2,3),若$\overrightarrow{AB}$=3$\overrightarrow a$,则点B的坐标是(5,8).
9.首项为-4的等差数列{an}从第10项起为正数,则公差d的取值范围为( )
| A. | $({\frac{4}{9},+∞})$ | B. | $({\frac{4}{9},\frac{1}{2}})$ | C. | $({\frac{4}{9},\frac{1}{2}}]$ | D. | $({-∞,\frac{4}{9}})$ |
7.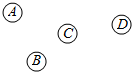 如图,A、B、C、D为四个村庄,要修筑三条公路,将这四个村庄连起来,则不同的修筑方法共有( )
如图,A、B、C、D为四个村庄,要修筑三条公路,将这四个村庄连起来,则不同的修筑方法共有( )
 如图,A、B、C、D为四个村庄,要修筑三条公路,将这四个村庄连起来,则不同的修筑方法共有( )
如图,A、B、C、D为四个村庄,要修筑三条公路,将这四个村庄连起来,则不同的修筑方法共有( )| A. | 8种 | B. | 12种 | C. | 16种 | D. | 20种 |