题目内容
【题目】已知函数
，在点
处的切线方程为
，求（1）实数
的值；（2）函数
的单调区间以及在区间
上的最值.
【答案】（1）
（2）
【解析】试题分析：（1）由题已知点
处的切线方程
，可获得两个条件；即：点
再函数的图像上，令点
处的导数为切线斜率。可得两个方程，求出
的值
（2）由（1）已知函数的解析式，可运用导数求出函数的单调区间和最值。即：
为函数的增区间，反之为减区间。最值需求出极值与区间端点值比较而得。
试题解析：（1）因为在点
处的切线方程为
，所以切线斜率是
，
且
，求得
，即点
，
又函数
，则
所以依题意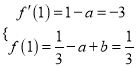得
，解得
（2）由（1）知
，所以
令
，解得
，当
；当
所以函数
的单调递增区间是
，单调递减区间是
又
，所以当x变化时，f（x）和f′（x）变化情况如下表：
X | 0 | （0,2） | 2 | （2,3） | 3 |
f′（x） | - | 0 | + | 0 | |
f（x） | 4 | ↘ | 极小值 | ↗ | 1 |
所以当
时， 
， 
练习册系列答案
点睛新教材全能解读系列答案
小学教材完全解读系列答案
相关题目
【题目】张三同学从7岁起到13岁每年生日时对自己的身高测量后记录如下表：
年龄 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
身高 | 121 | 128 | 135 | 141 | 148 | 154 | 160 |
（Ⅰ）求身高
关于年龄
的线性回归方程；
（Ⅱ）利用（Ⅰ）中的线性回归方程，分析张三同学7岁至13岁身高的变化情况，如17岁之前都符合这一变化，请预测张三同学15岁时的身高．
附：回归直线的斜率和截距的最小二乘法估计公式分别为：
，
．
