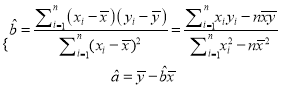题目内容
【题目】如图,在四棱锥PABCD中,侧面PAB⊥底面ABCD,底面ABCD为矩形,PA=PB,O为AB的中点,OD⊥PC.
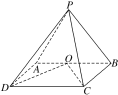
(1)求证:OC⊥PD;
(2)若PD与平面PAB所成的角为30°,求二面角DPCB的余弦值.
【答案】见解析
【解析】
解:(1)证明:连接OP,∵PA=PB,O为AB的中点,
∴OP⊥AB.
∵侧面PAB⊥底面ABCD,
∴OP⊥平面ABCD,
∴OP⊥OD,OP⊥OC.
∵OD⊥PC,OP∩PC=P,
∴OD⊥平面OPC,
∵OC平面OPC,∴OD⊥OC,
又OP⊥OC,OD∩OP=O,
∴OC⊥平面OPD,
∵PD平面OPD,∴OC⊥PD.
(2)取CD的中点E,以O为坐标原点,OE,OB,OP所在的直线分别为x轴,y轴,z轴建立空间直角坐标系Oxyz。
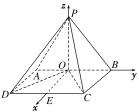
在矩形ABCD中,由(1)得OD⊥OC,
∴AB=2AD,不妨设AD=1,则AB=2。
∵侧面PAB⊥底面ABCD,底面ABCD为矩形,
∴DA⊥平面PAB,CB⊥平面PAB,△DPA≌△CPB,
∴∠DPA为直线PD与平面PAB所成的角,
∴∠DPA=30°,∠CPB=30°,PA=PB=![]() ,
,
∴B(0,1,0),C(1,1,0),D(1,-1,0),P(0,0,![]() ),从而
),从而![]() =(1,1,-
=(1,1,-![]() ),
),![]() =(0,-2,0).
=(0,-2,0).
设平面PCD的法向量为n1=(x1,y1,z1),
![]()
得![]()
可取n1=(![]() ,0,1).
,0,1).
同理,可取平面PCB的一个法向量为n2=(0,-![]() ,-1).
,-1).
于是cos〈n1,n2〉=![]() =-
=-![]() ,
,
∴二面角DPCB的余弦值为-![]() 。
。

【题目】葫芦岛市某高中进行一项调查:2012年至2016年本校学生人均年求学花销![]() (单位:万元)的数据如下表:
(单位:万元)的数据如下表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代号 | 1 | 2 | 3 | 4 | 5 |
年求学花销 | 3.2 | 3.5 | 3.8 | 4.6 | 4.9 |
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)利用(1)中的回归方程,分析2012年至2016年本校学生人均年求学花销的变化情况,并预测该地区2017年本校学生人均年求学花销情况.
附:回归直线的斜率和截距的最小二乘法估计公式分别为: