题目内容
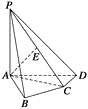
【题目】如图,在四棱锥P—ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
(1) 证明:AE⊥平面PCD;
(2) 求PB和平面PAD所成的角的大小.
【答案】(1)详见解析(2) 45°.
【解析】试题分析:(1) 要证明AE⊥平面PCD,只要证明AE⊥PC,结合AE⊥CD,即可证明结论;(2) 求PB和平面PAD所成的角的大小,说明∠APB就是要求的角即可求解
试题解析:(1)证明 在四棱锥P—ABCD中,因为PA⊥底面ABCD,CD平面ABCD,
故CD⊥PA.…1分 由条件CD⊥AC,PA∩AC=A,…2分 ∴CD⊥平面PAC.…3分
又AE平面PAC,∴AE⊥CD.…4分由PA=AB=BC,∠ABC=60°,可得AC=PA.…5分
∵E是PC的中点,∴AE⊥PC.…6分 又PC∩CD=C,综上得AE⊥平面PCD.…7分
(2)在四棱锥P—ABCD中,因为PA⊥底面ABCD,AB平面ABCD,故PA⊥AB.…8分
又AB⊥AD,PA∩AD=A,则 AB⊥平面PAD,…9分 故PB在平面PAD内的射影为PA,则∠APB为PB和平面PAD所成的角.……10分 在Rt△PAB中,AB=PA,
故∠APB=45°.…11分所以PB和平面PAD所成的角的大小为45°.……12分

练习册系列答案
相关题目