题目内容
11.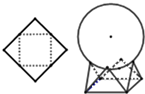 如图,用一边长为$\sqrt{2}$的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,将体积为$\frac{4}{3}$π的鸡蛋(视为球体)放入其中,蛋巢形状保持不变,则鸡蛋最高点与蛋巢底面的距离为 ( )
如图,用一边长为$\sqrt{2}$的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,将体积为$\frac{4}{3}$π的鸡蛋(视为球体)放入其中,蛋巢形状保持不变,则鸡蛋最高点与蛋巢底面的距离为 ( )| A. | $\frac{\sqrt{6}}{2}+\frac{3}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{{\sqrt{2}}}{2}+\frac{3}{2}$ | D. | $\frac{\sqrt{3}}{2}$+$\frac{3}{2}$ |
分析 有条件利用球的截面的性质求得球心到截面圆的距离,再求出垂直折起的4个小直角三角形的高,再与球的半径相加即得答案.
解答 解:由题意可得,蛋巢的底面是边长为1的正方形,
故经过4个顶点截鸡蛋所得的截面圆的直径为1,
由于鸡蛋的体积为$\frac{4}{3}$π,故鸡蛋(球)的半径为1,
故球心到截面圆的距离为$\sqrt{1-(\frac{1}{2})^{2}}$=$\frac{\sqrt{3}}{2}$,
而垂直折起的4个小直角三角形的高为$\frac{1}{2}$,
故鸡蛋最高点与蛋巢底面的距离为$\frac{\sqrt{3}}{2}$+1+$\frac{1}{2}$=$\frac{\sqrt{3}}{2}+\frac{3}{2}$,
故选:D
点评 本题主要考查球的截面的性质,图形的折叠问题,点、线、面间的位置关系,属于中档题

练习册系列答案
相关题目
16.具有线性相关关系得变量x,y,满足一组数据如表所示,若y与x的回归直线方程为$\widehat{y}$=3x-$\frac{3}{2}$,则m的值( )
| x | 0 | 1 | 2 | 3 |
| y | -1 | 1 | m | 8 |
| A. | 4 | B. | $\frac{9}{2}$ | C. | 5 | D. | 6 |
20.已知随机变量X服从正态分布N(1,σ2),且P(X≤0)=0.1,则P(X>2)=( )
| A. | 0.9 | B. | 0.1 | C. | 0.6 | D. | 0.4 |
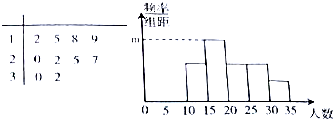 从某校随机抽取10个班,调查各班中有网购经历的人数,所得数据的茎叶图和频率分布直方图如图所示.(分组区间依次为[10,15),[15,20),[20,25),[25,30),[30,35))
从某校随机抽取10个班,调查各班中有网购经历的人数,所得数据的茎叶图和频率分布直方图如图所示.(分组区间依次为[10,15),[15,20),[20,25),[25,30),[30,35)) 已知F1,F2分别为椭圆C1:$\frac{y^2}{a^2}+\frac{x^2}{b^2}$=1的上、下焦点,F1是抛物线C1:x2=4y的焦点,点M是C1与C2在第二象限的交点,且|MF1|=$\frac{5}{3}$
已知F1,F2分别为椭圆C1:$\frac{y^2}{a^2}+\frac{x^2}{b^2}$=1的上、下焦点,F1是抛物线C1:x2=4y的焦点,点M是C1与C2在第二象限的交点,且|MF1|=$\frac{5}{3}$