题目内容
2.数列{an}的前n项和是Sn,若数列{an}的各项按如下规则排列:$\frac{1}{2}$,$\frac{1}{3}$,$\frac{2}{3}$,$\frac{1}{4}$,$\frac{2}{4}$,$\frac{3}{4}$,$\frac{1}{5}$,$\frac{2}{5}$,$\frac{3}{5}$,$\frac{4}{5}$,…,$\frac{1}{n}$,$\frac{2}{n}$,…,$\frac{n-1}{n}$,…,有如下运算和结论:①a23=$\frac{3}{8}$;
②S11=$\frac{31}{6}$;
③数列a1,a2+a3,a4+a5+a6,a7+a8+a9+a10,…是等比数列;
④数列a1,a2+a3,a4+a5+a6,a7+a8+a9+a10,…的前n项和Tn=$\frac{{n}^{2}+n}{4}$;
在横线上填写出所有你认为是正确的运算结果或结论的序号②④.
分析 将数列的项进行重新分组,结合等差数列的性质分别进行判断即可.
解答 解:由题意可得,分母为2的有一个,分母为3的有2个,分母为4的有3个,分母为5的有4个,分母为6的有5个,…
由于1+2+3+4+5+6=21,
故a23是分母为8的第二个,即a23=$\frac{2}{8}$.故①错误,
把原数列分组,分母相同的为一组:($\frac{1}{2}$);($\frac{1}{3}$,$\frac{2}{3}$);($\frac{1}{4}$,$\frac{2}{4}$,$\frac{3}{4}$);($\frac{1}{5}$,$\frac{2}{5}$,$\frac{3}{5}$,$\frac{4}{5}$);$\frac{1}{6}$…;
发现他们的个数是1,2,3,4,5…,
构建新数列{bn}表示数列中每一组的和,则bn=$\frac{1}{n+1}+\frac{2}{n+1}+…+\frac{n}{n+1}$=$\frac{\frac{(n+1)n}{2}}{n+1}$=$\frac{n}{2}$是个等差数列,
记bn的前n项和为Tn,
则S11=T4+a11=$\frac{1}{2}+\frac{2}{2}+\frac{3}{2}+\frac{4}{2}$+$\frac{1}{6}$=$\frac{31}{6}$;故②正确,
由②知{bn}为等差数列,故③错误,
由②知{bn}为等差数列,且故bn=$\frac{1}{n+1}+\frac{2}{n+1}+…+\frac{n}{n+1}$=$\frac{\frac{(n+1)n}{2}}{n+1}$=$\frac{n}{2}$,
则前n项和Tn=$\frac{(\frac{1}{2}+\frac{n}{2})n}{2}$=$\frac{{n}^{2}+n}{4}$,故④正确,
故正确的是②④
故答案为:②④
点评 本题目主要考查学生对数列的观察能力,找出数列之间的相互关系,根据等差数列的前n项和计算公式,根据已有条件计算.考查学生的计算能力以及对问题的分析能力.

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案| A. | [1,0] | B. | $[-1,\frac{4}{5}]$ | C. | $[-\frac{4}{5},1]$ | D. | [0,1] |
| A. | 3$\sqrt{3}$ | B. | $\frac{11}{2}$ | C. | ±3$\sqrt{3}$ | D. | 以上皆非 |
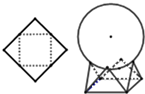 如图,用一边长为$\sqrt{2}$的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,将体积为$\frac{4}{3}$π的鸡蛋(视为球体)放入其中,蛋巢形状保持不变,则鸡蛋最高点与蛋巢底面的距离为 ( )
如图,用一边长为$\sqrt{2}$的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,将体积为$\frac{4}{3}$π的鸡蛋(视为球体)放入其中,蛋巢形状保持不变,则鸡蛋最高点与蛋巢底面的距离为 ( )| A. | $\frac{\sqrt{6}}{2}+\frac{3}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{{\sqrt{2}}}{2}+\frac{3}{2}$ | D. | $\frac{\sqrt{3}}{2}$+$\frac{3}{2}$ |
