题目内容
1.已知定义在R上的函数f(x)=|x+1|-|x-2|的最小值为a.(1)求a的值;
(2)若实数p,q,r满足p-2q+3r=a,求p2+q2+r2的最小值及取得最小值时对应的p,q,r的值.
分析 (1)由条件利用绝对值三角不等式,求得数f(x)=|x+1|-|x-2|的最小值,即可求得a的值.
(2)由条件利用柯西不等式,求得p2+q2+r2的最小值及取得最小值时对应的p,q,r的值.
解答 解:(1)∵||x+1|-|x-2||≤|(x+1)-(x-2)|=3,∴-3≤|x+1|-|x-2|≤3,
从而可得数f(x)=|x+1|-|x-2|的最小值为a=-3.
(2)由(1)知:p-2q+3r=-3,又(p2+q2+r2)•[12+(-2)2+32]≥(p-2q+3r)2 =9,
∴$p{\;}^2+q{\;}^2+r{\;}^2≥\frac{9}{14}$,当且仅当$\frac{p}{1}=\frac{q}{-2}=\frac{r}{3}即p=-\frac{3}{14},q=\frac{3}{7},r=-\frac{9}{14}时取等$,
故p2+q2+r2的最小值为$\frac{9}{14}$,此时$p=-\frac{3}{14},q=\frac{3}{7},r=-\frac{9}{14}$.
点评 本题主要考查绝对值三角不等式,柯西不等式的应用,属于基础题.

练习册系列答案
相关题目
13.正方形ABCD的边长为2,E是线段CD的中点,F是线段BE上的动点,则$\overrightarrow{BF}•\overrightarrow{FC}$的取值范围是( )
| A. | [1,0] | B. | $[-1,\frac{4}{5}]$ | C. | $[-\frac{4}{5},1]$ | D. | [0,1] |
10.在等比数列{an}中,a3,a9是方程3x2-11x+9=0的两个根,则a5a6a7=( )
| A. | 3$\sqrt{3}$ | B. | $\frac{11}{2}$ | C. | ±3$\sqrt{3}$ | D. | 以上皆非 |
11.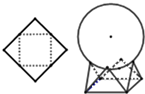 如图,用一边长为$\sqrt{2}$的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,将体积为$\frac{4}{3}$π的鸡蛋(视为球体)放入其中,蛋巢形状保持不变,则鸡蛋最高点与蛋巢底面的距离为 ( )
如图,用一边长为$\sqrt{2}$的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,将体积为$\frac{4}{3}$π的鸡蛋(视为球体)放入其中,蛋巢形状保持不变,则鸡蛋最高点与蛋巢底面的距离为 ( )
 如图,用一边长为$\sqrt{2}$的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,将体积为$\frac{4}{3}$π的鸡蛋(视为球体)放入其中,蛋巢形状保持不变,则鸡蛋最高点与蛋巢底面的距离为 ( )
如图,用一边长为$\sqrt{2}$的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,将体积为$\frac{4}{3}$π的鸡蛋(视为球体)放入其中,蛋巢形状保持不变,则鸡蛋最高点与蛋巢底面的距离为 ( )| A. | $\frac{\sqrt{6}}{2}+\frac{3}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{{\sqrt{2}}}{2}+\frac{3}{2}$ | D. | $\frac{\sqrt{3}}{2}$+$\frac{3}{2}$ |
 某海域的东西方向上分别有A,B两个观测点(如图),它们相距5(3+$\sqrt{3}$)海里.现有一艘轮船在D点发出求救信号,经探测得知D点位于A点北偏东45°,B点北偏西60°,这时,位于B点南偏西60°且与B点相距20$\sqrt{3}$海里的C点有一救援船,其航行速度为30海里/小时.
某海域的东西方向上分别有A,B两个观测点(如图),它们相距5(3+$\sqrt{3}$)海里.现有一艘轮船在D点发出求救信号,经探测得知D点位于A点北偏东45°,B点北偏西60°,这时,位于B点南偏西60°且与B点相距20$\sqrt{3}$海里的C点有一救援船,其航行速度为30海里/小时.