题目内容
6．下列类比推理的结论正确的是（ ）①类比“实数的乘法运算满足结合律”，得到猜想“向量的数量积运算满足结合律”；
②类比“平面内，同垂直于一直线的两直线相互平行”，得到猜想“空间中，同垂直于一直线的两直线相互平行”；
③类比“设等差数列{an}的前n项和为Sn，则S4，S8-S4，S12-S8成等差数列”，得到猜想“设等比数列{bn}的前n项积为Tn，则T4，$\frac{{T}_{8}}{{T}_{4}}$，$\frac{{T}_{12}}{{T}_{8}}$成等比数列”；
④类比“设AB为圆的直径，p为圆上任意一点，直线PA，PB的斜率存在，则kPA．kPB为常数”，得到猜想“设AB为椭圆的长轴，p为椭圆上任意一点，直线PA，PB的斜率存在，则kPA．kPB为常数”．
| A． | ①② | B． | ③④ | C． | ①④ | D． | ②③ |
分析 $\overrightarrow{a}$•（$\overrightarrow{b}$•$\overrightarrow{c}$），（$\overrightarrow{a}$•$\overrightarrow{b}$）•$\overrightarrow{c}$，分别为与向量$\overrightarrow{a}$，$\overrightarrow{c}$共线的向量，当$\overrightarrow{a}$，$\overrightarrow{c}$方向不同时，向量的数量积运算结合律不成立；空间中，同垂直于一直线的两直线可能平行，可能相交，也可能异面；利用排除法可得答案．
解答 解：$\overrightarrow{a}•$（$\overrightarrow{b}$•$\overrightarrow{c}$）与向量$\overrightarrow{a}$共线，（$\overrightarrow{a}$••$\overrightarrow{b}$）•$\overrightarrow{c}$与向量$\overrightarrow{c}$共线，
当$\overrightarrow{a}$，$\overrightarrow{c}$方向不同时，向量的数量积运算结合律不成立，故①错误，可排除A，C答案；
空间中，同垂直于一直线的两直线可能平行，可能相交，也可能异面，故②错误，可排除D答案；
故选：B．
点评 本题考查的知识点是类比推理，其中利用排除法排除错误答案是解答选择题的常用技巧．
练习册系列答案
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案
名师指导一卷通系列答案
相关题目
某海域的东西方向上分别有A，B两个观测点（如图），它们相距5（3+$\sqrt{3}$）海里．现有一艘轮船在D点发出求救信号，经探测得知D点位于A点北偏东45°，B点北偏西60°，这时，位于B点南偏西60°且与B点相距20$\sqrt{3}$海里的C点有一救援船，其航行速度为30海里/小时．
11．
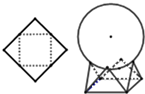如图，用一边长为$\sqrt{2}$的正方形硬纸，按各边中点垂直折起四个小三角形，做成一个蛋巢，将体积为$\frac{4}{3}$π的鸡蛋（视为球体）放入其中，蛋巢形状保持不变，则鸡蛋最高点与蛋巢底面的距离为 （ ）
如图，用一边长为$\sqrt{2}$的正方形硬纸，按各边中点垂直折起四个小三角形，做成一个蛋巢，将体积为$\frac{4}{3}$π的鸡蛋（视为球体）放入其中，蛋巢形状保持不变，则鸡蛋最高点与蛋巢底面的距离为 （ ）| A． | $\frac{\sqrt{6}}{2}+\frac{3}{2}$ | B． | $\frac{3}{2}$ | C． | $\frac{{\sqrt{2}}}{2}+\frac{3}{2}$ | D． | $\frac{\sqrt{3}}{2}$+$\frac{3}{2}$ |