Question

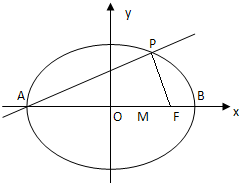
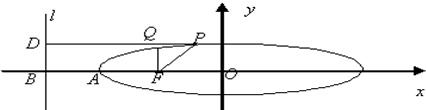
如图所示：椭圆的中心为O，F为焦点，A为顶点，准线L交OA的延长线于B，P、Q在椭圆上，且PD⊥L于D，QF⊥OA于F，椭圆的离心率为e，给出下列结论：
①e=

|PF|

|PD|

；②e=

|QF|

|BF|

；③e=

|AO|

|BO|

；④e=

|AF|

|PF|

；⑤e=

|FO|

|AO|

其中正确命题的序号是______（写出所有正确命题的序号）

Answer 1

设椭圆的方程为

x2

a2

+

y2

b2

=1，（0＜a＜b）依次分析5个比值的式子可得：
①、根据椭圆的第二定义，可得

|PF|

|PD|

=e，故符合；
②、根据椭圆的性质，可得|BF|=

a2

c

-c=

b2

c

，|QF|=

b2

a

，则

|QF|

|BF|

=

c

a

=e，故符合；
③、由椭圆的性质，可得|AO|=a，|BO|=

a2

c

，则

|AO|

|BO|

=

c

a

=e，故符合；
④、由椭圆的性质，可得|AF|=a-c，

|PF|

|PD|

=e|AF|≠|PD|，故不符合；
⑤、由椭圆的性质，可得|AO|=a，|FO|=c，

|FO|

|AO|

=

c

a

=e，故符合；
故答案为①②③⑤．