题目内容

在平面直角坐标系xOy中，已知椭圆
x2
4
+
y2
3
=1的左焦点为F，直线x-y-1=0，x-y+1=0与椭圆分别相交于点A，B，C，D，则AF+BF+CF+DF=______．
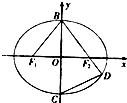
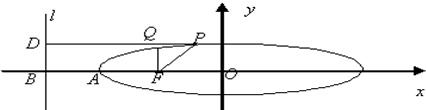
由题意，设椭圆的右焦点为F1，两条平行直线分别经过椭圆的两个焦点，连接AF，F1D．
由椭圆的对称性可知，四边形AFDF1（其中F1是椭圆的左焦点）为平行四边形，所以AF1=FD，同理BF1=CF
所以AF+BF+CF+DF=AF+BF+BF1+AF1=4a=8．
故答案为：8．
练习册系列答案
相关题目
如图，在平面直角坐标系xOy中，F1，F2分别为椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)的左、右焦点，B，C分别为椭圆的上、下顶点，直线BF2与椭圆的另一个交点为D，若cos∠F1BF2=
7
25
，则直线CD的斜率为______．
如图所示：椭圆的中心为O，F为焦点，A为顶点，准线L交OA的延长线于B，P、Q在椭圆上，且PD⊥L于D，QF⊥OA于F，椭圆的离心率为e，给出下列结论：
①e=
|PF|
|PD|
；②e=
|QF|
|BF|
；③e=
|AO|
|BO|
；④e=
|AF|
|PF|
；⑤e=
|FO|
|AO|

其中正确命题的序号是______（写出所有正确命题的序号）
已知△ABC的两个顶点A，B的坐标分别是（0，-1），（0，1），且AC，BC所在直线的斜率之积等于m（m≠0）．
（1）求顶点C的轨迹E的方程，并判断轨迹E为何种圆锥曲线；
（2）当m=-
1
2
时，过点F（1，0）的直线l交曲线E于M，N两点，设点N关于x轴的对称点为Q（M，Q不重合）试问：直线MQ与x轴的交点是否为定点？若是，求出定点，若不是，请说明理由．
设P是椭圆
x2
169
+
y2
144
=1上一点，F1、F2是椭圆的焦点，若|PF1|等于4，则|PF2|等于（　　）
A．22B．21C．20D．13
已知F1，F2是椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)的两个焦点，AB是过F1的弦，则△ABF2的周长是（　　）
A．2aB．4aC．8aD．2a+2b
已知动点P在椭圆
x2
25
+
y2
16
=1上，若A点坐标为（3，0），且|
AM
|=1，且
PM
•
AM
=0，则|
PM
|的最小值是（　　）
A．
2
B．
3
C．2D．3
已知有公共焦点的椭圆与双曲线的中心为原点，焦点在x轴上，左、右焦点分别为F1，F2且它们在第一象限的交点为P，△PF1F2是以PF1为底边的等腰三角形，双曲线的离心率的取值范围为（1，2），则该椭圆的离心率的取值范围是（　　）
A．（0，
1
3
）		B．（
1
3
，
1
2
）		C．（
1
3
，
2
5
）		D．（
2
5
，1）
设椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)的右焦点为F，C为椭圆短轴上的端点，向量
FC
绕F点顺时针旋转90°后得到向量
FC′
，其中C′点恰好落在椭圆右准线上，则该椭圆的离心率为______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网