题目内容
【题目】在四棱锥P﹣ABCD中,底面四边形ABCD是一个菱形,且∠ABC![]() ,AB=2,PA⊥平面ABCD.
,AB=2,PA⊥平面ABCD.
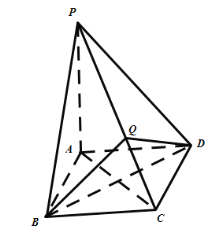
(1)若Q是线段PC上的任意一点,证明:平面PAC⊥平面QBD.
(2)当平面PBC与平面PDC所成的锐二面角的余弦值为![]() 时,求PA的长.
时,求PA的长.
【答案】(1)见解析(2)![]()
【解析】
(1)先证明BD⊥平面PAC,再由面面垂直的判定定理即可得证;
(2)建立空间直角坐标系,设P(0,![]() 1,a)(a>0),求出平面PBC与平面PDC的法向量,利用向量夹角公式建立关于a的方程,解出即可.
1,a)(a>0),求出平面PBC与平面PDC的法向量,利用向量夹角公式建立关于a的方程,解出即可.
(1)证明:∵四边形ABCD是一个菱形,∴AC⊥BD,
又PA⊥平面ABCD,∴PA⊥BD,
又AC∩PA=A,则BD⊥平面PAC,
∵BD在平面QBD内,
∴平面PAC⊥平面QBD;
(2)设AC,BD交于点O,分别以OB,OC所在直线为x轴,y轴,以平行于AP的直线为z轴建立如图所示的空间直角坐标系,
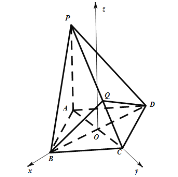
则![]() ,设P(0,
,设P(0,![]() 1,a)(a>0),
1,a)(a>0),
则![]() ,
,
设平面PBC的一个法向量为![]() ,
,
则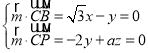 ,则
,则![]() ,
,
同理可求平面PDC的一个法向量为![]() ,
,
∴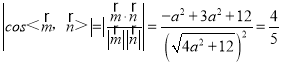 ,解得a2=2,
,解得a2=2,
∴![]() .
.

【题目】随着智能手机的普及,手机计步软件迅速流行开来,这类软件能自动记载每个人每日健步的步数,从而为科学健身提供一定的帮助.某市工会为了解该市市民每日健步走的情况,从本市市民中随机抽取了2000名市民(其中不超过40岁的市民恰好有1000名),利用手机计步软件统计了他们某天健步的步数,并将样本数据分为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
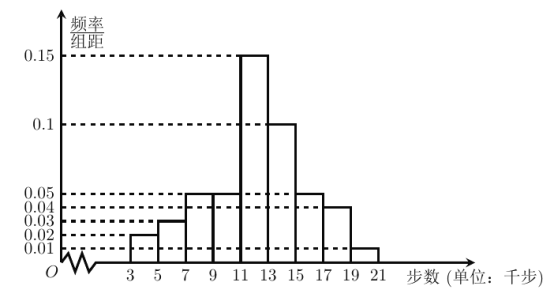
,![]() 九组(单位;千步),将抽取的不超过40岁的市民的样本数据绘制成频率分布直方图如图,将40岁以上的市民的样本数据绘制成频数分布表如下,并利用该样本的频率分布估计总体的概率分布.
九组(单位;千步),将抽取的不超过40岁的市民的样本数据绘制成频率分布直方图如图,将40岁以上的市民的样本数据绘制成频数分布表如下,并利用该样本的频率分布估计总体的概率分布.
分组(单位 千步) |
|
|
|
|
|
|
|
|
|
频数 | 10 | 20 | 20 | 30 | 400 | 200 | 200 | 100 | 20 |
(1)现规定,日健步步数不低于13000步的为“健步达人”,填写下面列联表,并根据列联表判断能否有99.9%的把握认为是否为“健步达人”与年龄有关;
健步达人 | 非健步达人 | 总计 | |
40岁以上的市民 | |||
不超过40岁的市民 | |||
总计 |
(2)利用样本平均数和中位数估计该市不超过40岁的市民日健步步数(单位:千步)的平均数和中位数;
(3)若日健步步数落在区间![]() 内,则可认为该市民”运动适量”,其中
内,则可认为该市民”运动适量”,其中![]() ,
,![]() 分别为样本平均数和样本标准差,计算可求得频率分布直方图中数据的标准差
分别为样本平均数和样本标准差,计算可求得频率分布直方图中数据的标准差![]() 约为3.64.若一市民某天的健步步数为2万步,试判断该市民这天是否“运动适量”?
约为3.64.若一市民某天的健步步数为2万步,试判断该市民这天是否“运动适量”?
参考公式: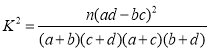
![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
【题目】千百年来,我国劳动人民在生产实践中根据云的形状、走向、速度、厚度、颜色等的变化,总结了丰富的“看云识天气”的经验,并将这些经验编成谚语,如“天上钩钩云,地上雨淋淋”“日落云里走,雨在半夜后”……小波同学为了验证“日落云里走,雨在半夜后”,观察了所在地区![]() 的
的![]() 天日落和夜晚天气,得到如下
天日落和夜晚天气,得到如下![]() 列联表:
列联表:
夜晚天气日落云里走 | 下雨 | 未下雨 |
出现 |
|
|
未出现 |
|
|
参考公式: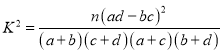 .
.
临界值表:
|
|
|
|
|
|
|
|
|
|
(1)根据上面的列联表判断能否有![]() 的把握认为“当晚下雨”与“‘日落云里走’出现”有关?
的把握认为“当晚下雨”与“‘日落云里走’出现”有关?
(2)小波同学为进一步认识其规律,对相关数据进行分析,现从上述调查的“夜晚未下雨”天气中按分层抽样法抽取![]() 天,再从这
天,再从这![]() 天中随机抽出
天中随机抽出![]() 天进行数据分析,求抽到的这
天进行数据分析,求抽到的这![]() 天中仅有
天中仅有![]() 天出现“日落云里走”的概率.
天出现“日落云里走”的概率.