题目内容
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)当![]() 时,讨论
时,讨论![]() 的单调性;
的单调性;
(3)若![]() 有两个极值点
有两个极值点![]() 、
、![]() ,且不等式
,且不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)见解析(3)
(2)见解析(3)![]()
【解析】
(1)先对函数求导,求出切线方程的斜率,再求出该点的函数值,利用点斜式求解;(2)利用导函数的正负判断原函数的单调性,再分类讨论;(3)从函数![]() 在
在![]() 上有两个极值点,根据韦达定理得到
上有两个极值点,根据韦达定理得到![]() 与
与![]() 的关系,分离出参数
的关系,分离出参数![]() ,从而得到关于
,从而得到关于![]() 的新函数,再求最值.
的新函数,再求最值.
解:(1)当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以,函数![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,即
,即![]() ;
;
(2)函数![]() 定义域为
定义域为![]() ,
,![]() ,
,
二次函数![]() 的判别式
的判别式![]() .
.
①若![]() 时,即当
时,即当![]() 时,对任意的
时,对任意的![]() ,
,![]() ,
,
此时,函数![]() 单调递增区间为
单调递增区间为![]() ,无减区间;
,无减区间;
②若![]() 时,即当
时,即当![]() 时,
时,
由![]() ,得
,得![]() 或
或![]() .
.
当![]() ,或
,或![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
此时,函数![]() 单调递增区间为
单调递增区间为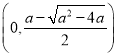 ,
,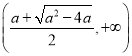 ,单调递减区间为
,单调递减区间为 ;
;
(3)由(2)知,![]() ,且
,且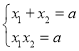 ,
,
不等式![]() 恒成立等价于
恒成立等价于![]() 恒成立,
恒成立,
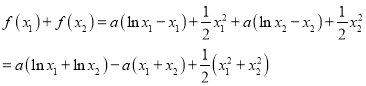
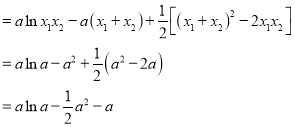
所以![]() ,
,
令![]() ,则
,则![]() ,
,
所以![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() ,所以
,所以![]() .
.
因此,实数![]() 的取值范围是
的取值范围是![]() .
.

【题目】绿水青山就是金山银山.某山村为做好水土保持,退耕还林,在本村的山坡上种植水果,并推出山村游等旅游项目.为预估今年7月份游客购买水果的情况,随机抽样统计了去年7月份100名游客的购买金额.分组如下:![]() ,
,![]() ,
,![]()
![]() ,得到如图所示的频率分布直方图:
,得到如图所示的频率分布直方图:
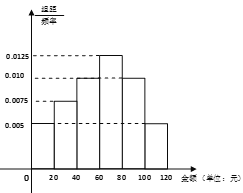
(1)请用抽样的数据估计今年7月份游客人均购买水果的金额(同一组中的数据用该组区间中点作代表).
(2)若把去年7月份购买水果不低于80元的游客,称为“水果达人”. 填写下面列联表,并根据列联表判断是否有95%的把握认为“水果达人”与性别有关系?
水果达人 | 非水果达人 | 合计 | |
男 | 10 | ||
女 | 30 | ||
合计 |
(3)为吸引顾客,商家特推出两种促销方案.方案一:每满80元可立减10元;方案二:金额超过80元可抽奖三次,每次中奖的概率为![]() ,且每次抽奖互不影响,中奖1次打9折,中奖2次打8折,中奖3次打7折.若每斤水果10元,你打算购买12斤水果,请从实际付款金额的数学期望的角度分析应该选择哪种优惠方案.
,且每次抽奖互不影响,中奖1次打9折,中奖2次打8折,中奖3次打7折.若每斤水果10元,你打算购买12斤水果,请从实际付款金额的数学期望的角度分析应该选择哪种优惠方案.
附:参考公式和数据:![]() ,
,![]() .临界值表:
.临界值表:
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 |
| 0.150 | 0.100 | 0.050 | 0.010 | 0.005 |