题目内容
【题目】已知函数f(x)=sin2xsin2x.
（1）讨论f(x)在区间(0，π)的单调性；
（2）证明：
；
（3）设n∈N*，证明：sin2xsin22xsin24x…sin22nx≤
.
【答案】（1）当
时，
单调递增，当
时，
单调递减，当
时，单调递增.（2）证明见解析；（3）证明见解析.
【解析】
(1)首先求得导函数的解析式，然后由导函数的零点确定其在各个区间上的符号，最后确定原函数的单调性即可；
(2)首先确定函数的周期性，然后结合(1)中的结论确定函数在一个周期内的最大值和最小值即可证得题中的不等式；
(3)对所给的不等式左侧进行恒等变形可得
，然后结合(2)的结论和三角函数的有界性进行放缩即可证得题中的不等式.
(1)由函数的解析式可得：
，则：
，
在
上的根为：
，
当时，单调递增，
当时，单调递减，
当时，单调递增.
(2)注意到
，
故函数
是周期为
的函数，
结合(1)的结论，计算可得：
，
，
，
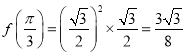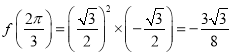据此可得：
，
，
即
.
(3)结合(2)的结论有：
.
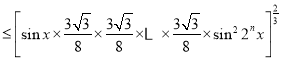
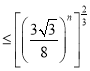
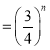练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
