ЬтФПФкШн
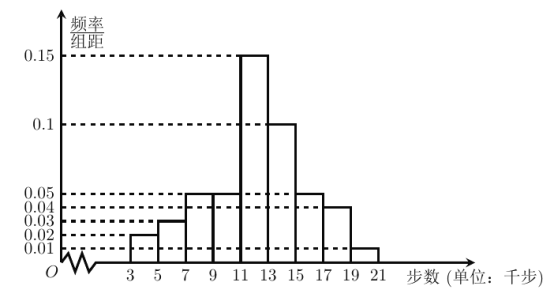
ЁОЬтФПЁПЫцзХжЧФмЪжЛњЕФЦеМАЃЌЪжЛњМЦВНШэМўбИЫйСїааПЊРДЃЌетРрШэМўФмздЖЏМЧдиУПИіШЫУПШеНЁВНЕФВНЪ§ЃЌДгЖјЮЊПЦбЇНЁЩэЬсЙЉвЛЖЈЕФАяжњ.ФГЪаЙЄЛсЮЊСЫНтИУЪаЪаУёУПШеНЁВНзпЕФЧщПіЃЌДгБОЪаЪаУёжаЫцЛњГщШЁСЫ2000УћЪаУёЃЈЦфжаВЛГЌЙ§40ЫъЕФЪаУёЧЁКУга1000УћЃЉЃЌРћгУЪжЛњМЦВНШэМўЭГМЦСЫЫћУЧФГЬьНЁВНЕФВНЪ§ЃЌВЂНЋбљБОЪ§ОнЗжЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
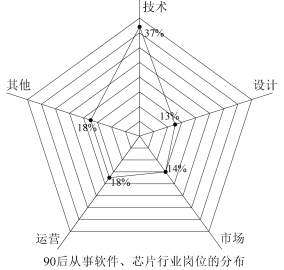
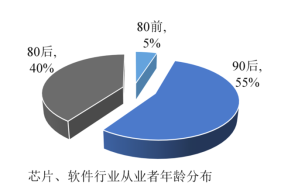
ЃЌ![]() ОХзщЃЈЕЅЮЛЃЛЧЇВНЃЉЃЌНЋГщШЁЕФВЛГЌЙ§40ЫъЕФЪаУёЕФбљБОЪ§ОнЛцжЦГЩЦЕТЪЗжВМжБЗНЭМШчЭМЃЌНЋ40ЫъвдЩЯЕФЪаУёЕФбљБОЪ§ОнЛцжЦГЩЦЕЪ§ЗжВМБэШчЯТЃЌВЂРћгУИУбљБОЕФЦЕТЪЗжВМЙРМЦзмЬхЕФИХТЪЗжВМ.
ОХзщЃЈЕЅЮЛЃЛЧЇВНЃЉЃЌНЋГщШЁЕФВЛГЌЙ§40ЫъЕФЪаУёЕФбљБОЪ§ОнЛцжЦГЩЦЕТЪЗжВМжБЗНЭМШчЭМЃЌНЋ40ЫъвдЩЯЕФЪаУёЕФбљБОЪ§ОнЛцжЦГЩЦЕЪ§ЗжВМБэШчЯТЃЌВЂРћгУИУбљБОЕФЦЕТЪЗжВМЙРМЦзмЬхЕФИХТЪЗжВМ.
ЗжзщЃЈЕЅЮЛ ЧЇВНЃЉ |
|
|
|
|
|
|
|
|
|
ЦЕЪ§ | 10 | 20 | 20 | 30 | 400 | 200 | 200 | 100 | 20 |
ЃЈ1ЃЉЯжЙцЖЈЃЌШеНЁВНВНЪ§ВЛЕЭгк13000ВНЕФЮЊЁАНЁВНДяШЫЁБЃЌЬюаДЯТУцСаСЊБэЃЌВЂИљОнСаСЊБэХаЖЯФмЗёга99.9%ЕФАбЮеШЯЮЊЪЧЗёЮЊЁАНЁВНДяШЫЁБгыФъСфгаЙиЃЛ
НЁВНДяШЫ | ЗЧНЁВНДяШЫ | змМЦ | |
40ЫъвдЩЯЕФЪаУё | |||
ВЛГЌЙ§40ЫъЕФЪаУё | |||
змМЦ |
ЃЈ2ЃЉРћгУбљБОЦНОљЪ§КЭжаЮЛЪ§ЙРМЦИУЪаВЛГЌЙ§40ЫъЕФЪаУёШеНЁВНВНЪ§ЃЈЕЅЮЛЃКЧЇВНЃЉЕФЦНОљЪ§КЭжаЮЛЪ§ЃЛ
ЃЈ3ЃЉШєШеНЁВНВНЪ§ТфдкЧјМф![]() ФкЃЌдђПЩШЯЮЊИУЪаУёЁБдЫЖЏЪЪСПЁБЃЌЦфжа
ФкЃЌдђПЩШЯЮЊИУЪаУёЁБдЫЖЏЪЪСПЁБЃЌЦфжа![]() ЃЌ
ЃЌ![]() ЗжБ№ЮЊбљБОЦНОљЪ§КЭбљБОБъзМВюЃЌМЦЫуПЩЧѓЕУЦЕТЪЗжВМжБЗНЭМжаЪ§ОнЕФБъзМВю
ЗжБ№ЮЊбљБОЦНОљЪ§КЭбљБОБъзМВюЃЌМЦЫуПЩЧѓЕУЦЕТЪЗжВМжБЗНЭМжаЪ§ОнЕФБъзМВю![]() дМЮЊ3.64.ШєвЛЪаУёФГЬьЕФНЁВНВНЪ§ЮЊ2ЭђВНЃЌЪдХаЖЯИУЪаУёетЬьЪЧЗёЁАдЫЖЏЪЪСПЁБЃП
дМЮЊ3.64.ШєвЛЪаУёФГЬьЕФНЁВНВНЪ§ЮЊ2ЭђВНЃЌЪдХаЖЯИУЪаУёетЬьЪЧЗёЁАдЫЖЏЪЪСПЁБЃП
ВЮПМЙЋЪНЃК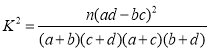
![]() .
.
ВЮПМЪ§ОнЃК
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
ЁОД№АИЁП(1)БэИёМћНтЮі,га99.9%ЕФАбЮеШЯЮЊЪЧЗёЮЊЁАНЁВНДяШЫЁБгыФъСфгаЙи;(2) 12.16,![]() ;(3) ИУЪаУёетЬь ЁАдЫЖЏВЛЪЪСПЁБ.
;(3) ИУЪаУёетЬь ЁАдЫЖЏВЛЪЪСПЁБ.
ЁОНтЮіЁП
(1)ИљОнвбжЊПЩЭъГЩБэИё,ИљОнБэИёЪ§ОнМЦЫу![]() МДПЩ;(2)ЭЈЙ§ЦЕТЪЗжВМжБЗНЭМжаЪ§ОнИљОнЖЈвхМЦЫуПЩЧѓГіЦНОљЪ§КЭжаЮЛЪ§;(3) гЩ
МДПЩ;(2)ЭЈЙ§ЦЕТЪЗжВМжБЗНЭМжаЪ§ОнИљОнЖЈвхМЦЫуПЩЧѓГіЦНОљЪ§КЭжаЮЛЪ§;(3) гЩ![]() ,ПЩжЊ
,ПЩжЊ![]() ЭђВНМД
ЭђВНМД![]() ЧЇВНВЛдкЧјМфЗЖЮЇФк,МДПЩЕУГіНсТл.
ЧЇВНВЛдкЧјМфЗЖЮЇФк,МДПЩЕУГіНсТл.
(1)СаСЊБэЮЊ
НЁВНДяШЫ | ЗЧНЁВНДяШЫ | змМЦ | |
40ЫъвдЩЯЕФЪаУё | 520 | 480 | 1000 |
ВЛГЌЙ§40ЫъЕФЪаУё | 400 | 600 | 1000 |
змМЦ | 920 | 1080 | 2000 |
![]() .
.
Ыљвдга99.9%ЕФАбЮеШЯЮЊЪЧЗёЮЊЁАНЁВНДяШЫЁБгыФъСфгаЙи.
(2)бљБОЦНОљЪ§ЮЊ![]()
гЩЧАЫФзщЕФЦЕТЪжЎКЭЮЊ![]() ,ЧАЮхзщЕФЦЕТЪжЎКЭЮЊ
,ЧАЮхзщЕФЦЕТЪжЎКЭЮЊ![]() ,жЊбљБОжаЮЛЪ§ТфдкЕкЮхзщ,ЩшбљБОжаЮЛЪ§ЮЊ
,жЊбљБОжаЮЛЪ§ТфдкЕкЮхзщ,ЩшбљБОжаЮЛЪ§ЮЊ![]() ,дђ
,дђ![]() .ЙЪПЩвдЙРМЦ,ИУЪаВЛГЌЙ§40ЫъЕФЪаУёШеНЁВНВНЪ§ЕФЦНОљЪ§ЮЊ12.16КЭжаЮЛЪ§
.ЙЪПЩвдЙРМЦ,ИУЪаВЛГЌЙ§40ЫъЕФЪаУёШеНЁВНВНЪ§ЕФЦНОљЪ§ЮЊ12.16КЭжаЮЛЪ§![]() .
.
(3) ![]() ,Жј
,Жј![]() ЭђВНЧЁКУТфдкИУЧјМфгвВр,ЫљвдПЩОнДЫИУЪаУёетЬь ЁАдЫЖЏВЛЪЪСПЁБ.
ЭђВНЧЁКУТфдкИУЧјМфгвВр,ЫљвдПЩОнДЫИУЪаУёетЬь ЁАдЫЖЏВЛЪЪСПЁБ.