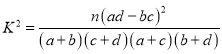题目内容
【题目】已知![]() 的内角
的内角![]() 、
、![]() 、
、![]() 的对边分别为
的对边分别为![]() 、
、![]() 、
、![]() ,且
,且![]() .
.
(Ⅰ)求![]() ;
;
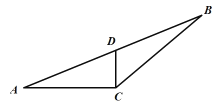
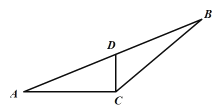
(Ⅱ)若![]() ,
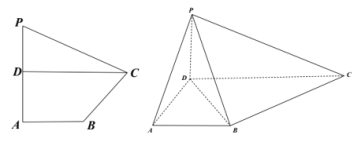
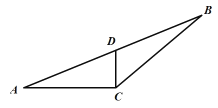
,![]() ,如图,
,如图,![]() 为线段
为线段![]() 上一点,且
上一点,且![]() ,求
,求![]() 的长.
的长.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
【解析】
(Ⅰ)根据正弦定理和余弦定理进行求解即可.
(Ⅱ)根据(Ⅰ)式和余弦定理可求得![]() ,然后根据余弦定理可求得
,然后根据余弦定理可求得![]() ,进而可以利用辅助角公式求出
,进而可以利用辅助角公式求出![]() ,进而求出
,进而求出![]() 和
和![]() .
.
(Ⅰ)解法1:根据正弦定理,由![]() 得
得
![]() ,
,
整理得![]() .
.
因为![]() ,所以
,所以![]() .
.
解法2:由![]() 得
得![]() ,
,
由余弦定理得:![]() ,
,
整理得![]() ,
,![]() .
.
所以![]() .
.
(Ⅱ)解法1:在![]() 中,由余弦定理得:
中,由余弦定理得:![]() ,
,
整理得![]() ,解得
,解得![]() 或
或![]() (舍),即
(舍),即![]() .
.
在![]() 中,由(1)结论可知:
中,由(1)结论可知:![]() .
.
由正弦定理得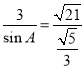 ,所以
,所以![]() ,
,
由(Ⅰ)结论可得出![]() 为锐角,所以
为锐角,所以![]() ,
,![]() ,
,
在![]() 中,
中,![]() .
.
解法2:在![]() 中,由余弦定理得:
中,由余弦定理得:![]() ,
,
将(Ⅰ)中所求代入整理得:![]() ,解得
,解得![]() 或
或![]() (舍),即
(舍),即![]() .
.
在![]() 中,由余弦定理可知:
中,由余弦定理可知:![]() ,
,
所以![]() ,
,![]() ,
,
在![]() 中,
中,![]() .
.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目