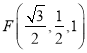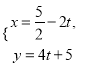题目内容
【题目】已知函数![]() ,
, ![]() 为自然对数的底数,
为自然对数的底数, ![]() .
.
(1)试讨论函数![]() 的单调性;
的单调性;
(2)当![]() 时,
时, ![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1) 当![]() 时,
时, ![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时,
时, ![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(2) ![]() .
.
【解析】试题分析:(1)对函数求导,关注定义域,对参数 a进行讨论,得出函数的单调性;(2)解决恒成立的最基本方法就是分离参数,化为![]() 对
对![]() 时恒成立.设右边为函数g(x),通过两次求导研究函数g(x)的单调性和最大值,最后利用极值原理得出a的范围.
时恒成立.设右边为函数g(x),通过两次求导研究函数g(x)的单调性和最大值,最后利用极值原理得出a的范围.
试题解析:
(1)![]() 的定义域为
的定义域为![]() ,
, ![]() .
.
若![]() 时,则
时,则![]() ,∴
,∴![]() 在
在![]() 上单调递增;
上单调递增;
若![]() 时,则由
时,则由![]() ,∴
,∴![]() .
.
当![]() 时,
时, ![]() ,∴
,∴![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时, ![]() ,∴
,∴![]() 在
在![]() 上单调递减.
上单调递减.
综上所述,当![]() 时,
时, ![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时, ![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(2)由题意得: ![]() 对
对![]() 时恒成立,
时恒成立,
∴![]() 对
对![]() 时恒成立.
时恒成立.
令![]() ,(
,( ![]() ),
),
∴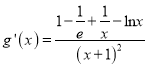 .
.
令![]() ,
,
∴![]() 对
对![]() 时恒成立,
时恒成立,
∴![]() 在
在![]() 上单调递减,
上单调递减,
∵![]() ,
,
∴当![]() 时,
时, ![]() ,∴
,∴![]() ,
, ![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时, ![]() ,∴
,∴![]() ,
, ![]() 在
在![]() 上单调递减.
上单调递减.
∴![]() 在
在![]() 处取得最大值
处取得最大值![]() ,
,
∴![]() 的取值范围是
的取值范围是![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】已知数列{an}的各项均为正数,Sn是数列{an}的前n项和,且4Sn=an2+2an﹣3.
(1)求数列{an}的通项公式;
(2)已知bn=2n,求Tn=a1b1+a2b2+…+anbn的值.
【题目】随着经济的发展,某城市的市民收入逐年增长,表1是该城市某银行连续五年的储蓄存款额(年底余额):
表1
年份x | 2011 | 2012 | 2013 | 2014 | 2015 |
储蓄存款额y(千亿元) | 5 | 6 | 7 | 8 | 10 |
为了研究计算的方便,工作人员将表1的数据进行了处理,令t=x-2 010,z=y-5,得到表2:
表2
时间代号t | 1 | 2 | 3 | 4 | 5 |
z | 0 | 1 | 2 | 3 | 5 |
(1)z关于t的线性回归方程是________;y关于x的线性回归方程是________;
(2)用所求回归方程预测到2020年年底,该银行储蓄存款额可达________千亿元.
(附:线性回归方程![]() =
=![]() x+
x+![]() ,其中
,其中![]() =
=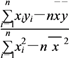 ,
,![]() =
=![]() -
-![]()
![]() )
)