Question

【题目】已知圆过， 两点，且圆心在直线上.

（1）求圆的方程；

（2）若直线过点且被圆截得的线段长为，求的方程.

Answer 1

【答案】（1）；（2）或

【解析】试题分析：（1）把点P、Q的坐标和圆心坐标代入圆的一般方程，利用待定系数法求得系数的值；（2）分类讨论，斜率存在和斜率不存在两种情况．①当直线l的斜率不存在时，满足题意，易得直线方程；②当直线l的斜率存在时，设所求直线l的斜率为k，则直线l的方程为：y-5=kx，由点到直线的距离公式求得k的值．

试题解析：

（1）设圆的方程为，圆心 ，根据题意有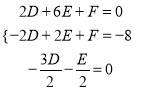，计算得出，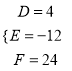

故所求圆的方程为.

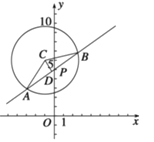
（2）如图所示， ，设是线段的中点，

则，

∴， .

在中，可得.

当直线的斜率不存在时，满足题意，

此时方程为.

当直线的斜率存在时，设所求直线的斜率为，则直线的方程为： ，

即，由点到直线的距离公式：

，得，此时直线的方程为.

∴所求直线的方程为或