题目内容
6．已知函数f（x）=$\left\{{\begin{array}{l}{3x+2（{x＜1}）}\\{{x^2}+ax（{x≥1}）}\end{array}}$，若f（f（0））=a，则实数a=-4．分析 根据函数解析式求出f（0）的值，再代入f（f（0））=a列出方程求出a的值．
解答 解：由题意得，f（x）=$\left\{\begin{array}{l}{3x+2（x＜1）}\\{{x}^{2}+ax（x≥1）}\end{array}\right.$，
∴f（0）=2，则f（f（0））=f（2）=4+2a=a，解得a=-4，
故答案为：-4．
点评 本题考查分段函数的函数值，对于多层函数值应从内到外依次求值，属于基础题．
练习册系列答案
相关题目
如图，圆O的半径为2，P是圆O的直径AB延长线上的一点，BP=1，割线PCD交圆O于C、D两点，过P作FP⊥AP，交直线AC于点E，交直线AD于点F．
17．设点F为双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点，直线l过原点且与双曲线C相交于A，B两点，若双曲线C的右顶点M恰为△ABF的重心，则双曲线C的离心率为（ ）
| A． | $\frac{4}{3}$ | B． | $\frac{3}{2}$ | C． | 2 | D． | 3 |
14．某机构对儿童记忆能力x和识图能力y进行统计分析，得到如下数据：
由表中数据，求得线性回归方程为$\stackrel{∧}{y}$=$\frac{4}{5}$$\stackrel{∧}{x}$+$\stackrel{∧}{a}$（$\hat a=\overline y-\frac{4}{5}$$\overline x$），若某儿童记忆能力为12，则他识图能力为（ ）
| 记忆能力x | 4 | 6 | 8 | 10 |
| 识图能力y | 3 | 5 | 6 | 8 |
| A． | 9.2 | B． | 9.8 | C． | 9.5 | D． | 10 |
1．函数f（x）的图象如图所示，下列选项中正确的是（ ）
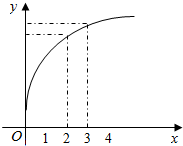
| A． | 0＜f′（2）＜f′（3）＜f（3）-f（2） | B． | 0＜f′（3）＜f′（2）＜f（3）-f（2） | C． | 0＜f′（3）＜f（3）-f（2）＜f′（2） | D． | 0＜f（3）-f（2）＜f′（2）＜f′（3） |
如图，已知A（10，0），直线x=t（0＜t＜10）与函数y=ex的图象交于点P，与x轴交于点H，记△APH的面积为f（t）．
15．sin120°=（ ）
| A． | -$\frac{1}{2}$ | B． | $\frac{1}{2}$ | C． | -$\frac{\sqrt{3}}{2}$ | D． | $\frac{\sqrt{3}}{2}$ |