题目内容
1.函数f(x)的图象如图所示,下列选项中正确的是( )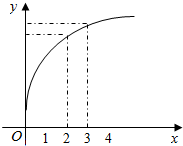
| A. | 0<f′(2)<f′(3)<f(3)-f(2) | B. | 0<f′(3)<f′(2)<f(3)-f(2) | C. | 0<f′(3)<f(3)-f(2)<f′(2) | D. | 0<f(3)-f(2)<f′(2)<f′(3) |
分析 利用图形f′(x)是单调递减函数,导数的概念,几何意义判断大小关系即可.
解答 解:根据导数的概念,几何意义得出:f′(3)以A(3,f(3))为切点的切线的斜率,
f′(2)以A(2,f(2))为切点的切线的斜率,
$\frac{f(3)-f(2)}{3-2}$为A(2,f(2)),B(3,f(3))的割线AB的斜率,
根据图形可判断f′(x)是单调递减函数,
故f′(3)<f(3)-f(2)<f′(2),
故选:C.
点评 本题考察了导数的概念,几何意义,数形结合的数学的运用,属于中档题.

练习册系列答案
相关题目
12.函数f(x)=$\frac{\sqrt{x}}{x-1}$的定义域是( )
| A. | [0,+∞) | B. | [0,1)∪(1,+∞) | C. | (0,1) | D. | (0,1)∪(1,+∞) |
9.如图是一个空间几何体的三视图,则该几何体的全面积为( )
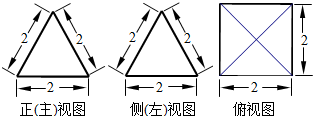

| A. | 12 | B. | 16 | C. | $\frac{{4\sqrt{3}}}{3}$+4 | D. | 4$\sqrt{3}$+4 |
13.如果cosα=$\frac{4}{5}$,那么$sin(α+\frac{π}{4})-\frac{{\sqrt{2}}}{2}$cosα等于( )
| A. | $\frac{{2\sqrt{2}}}{5}$ | B. | ±$\frac{{2\sqrt{2}}}{5}$ | C. | $\frac{{3\sqrt{2}}}{10}$ | D. | ±$\frac{{3\sqrt{2}}}{10}$ |
10.设f(x)是定义在R上的偶函数,对任意x∈R,都有f(x-1)=f(x+1),且当x∈[0,1]时,f(x)=1-3x,若在区间[-6,6]内关于x的方程f(x)-loga(x+3)=0(0<a<1)恰有5个不同的实数根,则a的取值范围是( )
| A. | $(\frac{{\sqrt{6}}}{6},\frac{1}{2})$ | B. | $(\frac{{\sqrt{6}}}{6},1)$ | C. | $(\frac{1}{2},1)$ | D. | $(\frac{1}{2},+∞)$ |