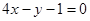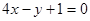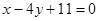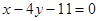题目内容
.设函数f(x)=g(x)+x2,曲线y=g(x)在点(1,g(1))处的切线方程为y=2x+1,则曲线y=f(x)在点(1,f(1))处切线的斜率为
A.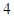 | B.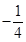 | C.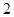 | D.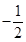 |
A
解:由题意,∵曲线y=g(x)在点(1,g(1))处的切线方程为y=2x+1
∴g′(1)=2
∵函数f(x)=g(x)+x2,
∴f′(x)=g′(x)+2x
∴f′(1)=g′(1)+2
∴f′(1)=2+2=4
∴曲线y=f(x)在点(1,f(1))处切线的斜率为4
故答案为A
∴g′(1)=2
∵函数f(x)=g(x)+x2,
∴f′(x)=g′(x)+2x
∴f′(1)=g′(1)+2
∴f′(1)=2+2=4
∴曲线y=f(x)在点(1,f(1))处切线的斜率为4
故答案为A

练习册系列答案
相关题目
 的导函数
的导函数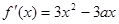 ,
,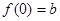 ,
,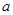 .
.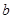 为实数.
为实数.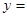
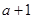 ,
,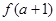 )处切线的斜率为12,求
)处切线的斜率为12,求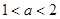 ,求函数
,求函数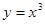 在点P处的切线的斜率等于3,则点P的坐标为( )
在点P处的切线的斜率等于3,则点P的坐标为( )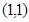 或
或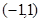
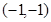 或
或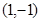
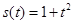 ,则运动开始后4s时物体的动能是( )(其中
,则运动开始后4s时物体的动能是( )(其中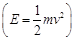 ).
).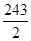 J
J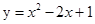 在点(2,2)处的切线方程为
在点(2,2)处的切线方程为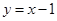
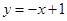
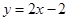

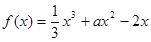 在区间
在区间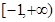 上有极大值和极小值,则实数
上有极大值和极小值,则实数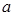 的取值范围是
的取值范围是 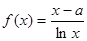 ,其中
,其中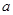 为实数.
为实数.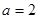 时,求曲线
时,求曲线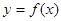 在点
在点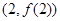 处的切线方程;
处的切线方程;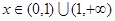 ,
,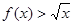 恒成立?若不存在,请说明理由,若存在,求出
恒成立?若不存在,请说明理由,若存在,求出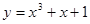 在点(1,3)处的切线方程是( )
在点(1,3)处的切线方程是( )