题目内容
(本题满分12分)
已知函数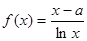 ,其中
,其中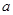 为实数.
为实数.
(Ⅰ)当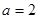 时,求曲线
时,求曲线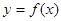 在点
在点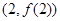 处的切线方程;
处的切线方程;
(Ⅱ)是否存在实数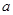 ,使得对任意
,使得对任意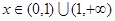 ,
,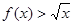 恒成立?若不存在,请说明理由,若存在,求出
恒成立?若不存在,请说明理由,若存在,求出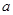 的值并加以证明.
的值并加以证明.
已知函数
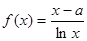 ,其中
,其中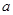 为实数.
为实数.(Ⅰ)当
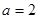 时,求曲线
时,求曲线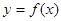 在点
在点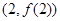 处的切线方程;
处的切线方程;(Ⅱ)是否存在实数
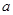 ,使得对任意
,使得对任意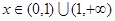 ,
,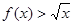 恒成立?若不存在,请说明理由,若存在,求出
恒成立?若不存在,请说明理由,若存在,求出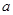 的值并加以证明.
的值并加以证明.(Ⅰ)
(Ⅱ)存在实数 ,使得对任意
,使得对任意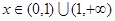 ,
,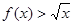 恒成立
恒成立

(Ⅱ)存在实数
 ,使得对任意
,使得对任意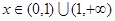 ,
,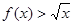 恒成立
恒成立本试题主要是考查了导数的几何意义的运用,以及运用导数求解函数的 最值综合运用。
(1)由已知关系式得到函数的定义域,然后把a=2代入原式中,求解函数的导数,利用函数在某点处的导数值即为该点的切线的斜率来求解得到切线方程。
(2)由于要是不等式恒成立,需要对原式进行变形,将分式转化为整式,然后构造函数求解最值得到参数的范围。
解:(Ⅰ)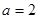 时,
时, ,
,
 ,
,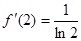 ,
,
又
所以切线方程为 ………6分
………6分
(Ⅱ)1°当 时,
时, ,则
,则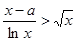

令 ,
,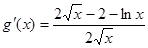 ,
,
再令 ,
,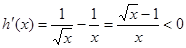
当 时
时 ,∴
,∴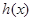 在
在 上递减,
上递减,
∴当 时,
时, ,
,
∴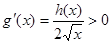 ,所以
,所以 在
在 上递增,
上递增, ,
,
所以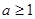
2° 时,
时, ,则
,则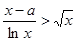


由1°知当 时
时 ,
,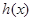 在
在 上递增
上递增
当 时,
时, ,
,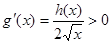
所以 在
在 上递增,∴
上递增,∴
∴ ;
;
由1°及2°得: ………12分
………12分
(1)由已知关系式得到函数的定义域,然后把a=2代入原式中,求解函数的导数,利用函数在某点处的导数值即为该点的切线的斜率来求解得到切线方程。
(2)由于要是不等式恒成立,需要对原式进行变形,将分式转化为整式,然后构造函数求解最值得到参数的范围。
解:(Ⅰ)
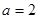 时,
时, ,
, ,
,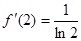 ,
,又

所以切线方程为
 ………6分
………6分(Ⅱ)1°当
 时,
时, ,则
,则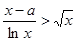

令
 ,
,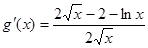 ,
,再令
 ,
,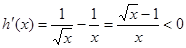
当
 时
时 ,∴
,∴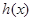 在
在 上递减,
上递减,∴当
 时,
时, ,
,∴
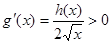 ,所以
,所以 在
在 上递增,
上递增, ,
,所以
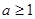
2°
 时,
时, ,则
,则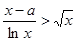


由1°知当
 时
时 ,
,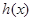 在
在 上递增
上递增当
 时,
时, ,
,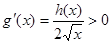
所以
 在
在 上递增,∴
上递增,∴
∴
 ;
;由1°及2°得:
 ………12分
………12分
练习册系列答案
相关题目
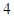
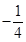
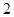
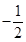
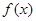 的定义域为
的定义域为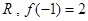 ,对任意
,对任意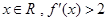 ,则
,则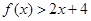 的解集为( )
的解集为( )
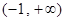
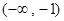
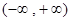
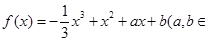
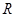 ).
).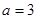 ,试确定函数
,试确定函数 的单调区间;
的单调区间;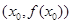 处切线的斜率都小于
处切线的斜率都小于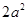 ,求实数
,求实数 的取值范围.
的取值范围.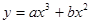 ,当
,当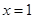 时,有极大值
时,有极大值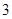 。
。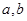 的值;
的值;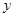 的极小值。
的极小值。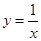 在点
在点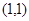 处的切线与直线
处的切线与直线 垂直,则
垂直,则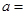 .
. 为曲线
为曲线 与
与 的公共点,且两条曲线在点
的公共点,且两条曲线在点 = .
= . 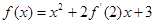 ,则
,则 .
.