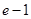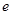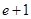题目内容
(本小题满分12分)已知三次函数 的导函数
的导函数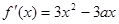 ,
,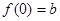 ,
,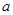 .
.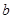 为实数.
为实数.
(1)若曲线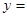
 在点(
在点(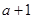 ,
,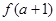 )处切线的斜率为12,求
)处切线的斜率为12,求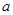 的值;
的值;
(2)若 在区间[-1,1]上的最小值.最大值分别为-2.1,且
在区间[-1,1]上的最小值.最大值分别为-2.1,且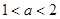 ,求函数
,求函数 的解析式.
的解析式.
 的导函数
的导函数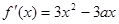 ,
,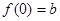 ,
,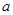 .
.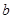 为实数.
为实数.(1)若曲线
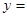
 在点(
在点(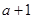 ,
,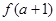 )处切线的斜率为12,求
)处切线的斜率为12,求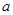 的值;
的值;(2)若
 在区间[-1,1]上的最小值.最大值分别为-2.1,且
在区间[-1,1]上的最小值.最大值分别为-2.1,且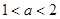 ,求函数
,求函数 的解析式.
的解析式.(Ⅰ)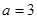 ;(Ⅱ)
;(Ⅱ) =
=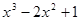 。
。
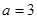 ;(Ⅱ)
;(Ⅱ) =
=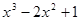 。
。(1)根据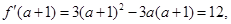 可得a值.
可得a值.
(2)由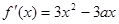 ,
,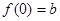 ,得
,得 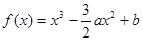
然后再根据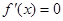 得x=0,x=a,再结合
得x=0,x=a,再结合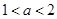 易求f(x)的单调区间,进而可得到其极值最值,从而得到关于a,b的方程,解出a值,b值,解析式确定.
易求f(x)的单调区间,进而可得到其极值最值,从而得到关于a,b的方程,解出a值,b值,解析式确定.
(Ⅰ)由导数的几何意义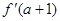 =12
=12
∴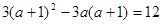
∴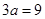 ∴
∴ 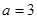 ………………………4分
………………………4分
(Ⅱ)∵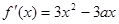 ,
,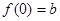 ∴
∴ 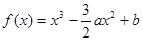
由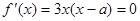 得
得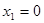 ,
,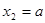
∵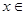 [-1,1],
[-1,1],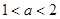
∴ 当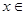 [-1,0)时,
[-1,0)时,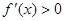 ,
, 递增;
递增;
当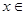 (0,1]时,
(0,1]时,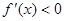 ,
, 递减.……………8分
递减.……………8分
∴ 在区间[-1,1]上的最大值为
在区间[-1,1]上的最大值为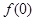
∵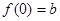 ,∴
,∴ 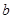 ="1" ……………………10分
="1" ……………………10分
∵ ,
,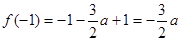
∴ ∴
∴ 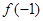 是函数
是函数 的最小值,
的最小值,
∴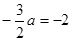 ∴
∴ 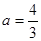
∴ =
=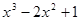 .................12分
.................12分
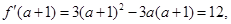 可得a值.
可得a值.(2)由
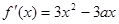 ,
,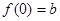 ,得
,得 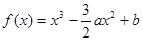
然后再根据
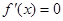 得x=0,x=a,再结合
得x=0,x=a,再结合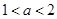 易求f(x)的单调区间,进而可得到其极值最值,从而得到关于a,b的方程,解出a值,b值,解析式确定.
易求f(x)的单调区间,进而可得到其极值最值,从而得到关于a,b的方程,解出a值,b值,解析式确定.(Ⅰ)由导数的几何意义
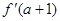 =12
=12 ∴
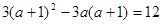
∴
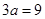 ∴
∴ 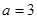 ………………………4分
………………………4分(Ⅱ)∵
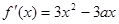 ,
,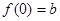 ∴
∴ 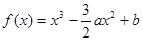
由
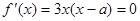 得
得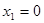 ,
,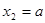
∵
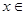 [-1,1],
[-1,1],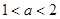
∴ 当
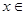 [-1,0)时,
[-1,0)时,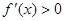 ,
, 递增;
递增;当
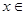 (0,1]时,
(0,1]时,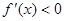 ,
, 递减.……………8分
递减.……………8分∴
 在区间[-1,1]上的最大值为
在区间[-1,1]上的最大值为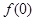
∵
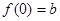 ,∴
,∴ 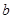 ="1" ……………………10分
="1" ……………………10分∵
 ,
,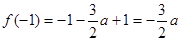
∴
 ∴
∴ 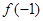 是函数
是函数 的最小值,
的最小值,∴
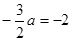 ∴
∴ 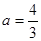
∴
 =
=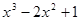 .................12分
.................12分
练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
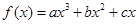 的极小值为
的极小值为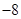 ,其导函数
,其导函数 的图像开口向下且经过点
的图像开口向下且经过点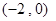 ,
,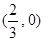 .
.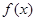 的解析式;(Ⅱ)方程
的解析式;(Ⅱ)方程 有唯一实数解,求
有唯一实数解,求 的取值范围.
的取值范围. 都有
都有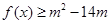 恒成立,求实数
恒成立,求实数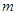 的取值范围.
的取值范围.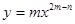 的导数为
的导数为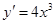 ,则( )
,则( )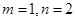
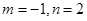
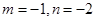
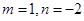
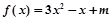 ,
,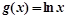 ,若函数
,若函数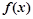 与
与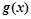 的图象在
的图象在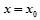 处的切线平行,则
处的切线平行,则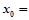 .
. 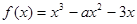 .
.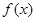 在
在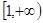 上是增函数,求实数
上是增函数,求实数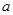 的取值范围;
的取值范围;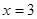 是
是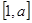 上的最小值和最大值.
上的最小值和最大值.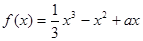 (
(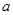 为常数)
为常数)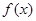 在区间
在区间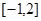 上单调递减,求
上单调递减,求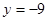 相切:
相切: 处取得极值,记点M (
处取得极值,记点M (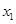 ,
,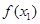 ),N(
),N(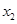 ,
,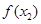 ),P(
),P(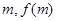 ),
), 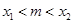 , 若对任意的m
, 若对任意的m  (
(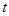 , x
, x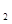 ),线段MP与曲线f(x)均有异于M,P的公共点,试确定
),线段MP与曲线f(x)均有异于M,P的公共点,试确定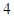
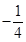
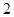
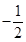
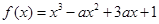 在区间
在区间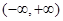 内既有极大值,又有极小值,
内既有极大值,又有极小值, 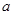 的取值范围是 .
的取值范围是 .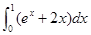 等于( )
等于( )