题目内容
13.正方体ABCD-A1B1C1D1的棱长为1,点M在$\overline{A{C}_{1}}$上且$\overrightarrow{AM}$=$\frac{1}{2}$$\overrightarrow{M{C}_{1}}$,N为B1B的中点,则|$\overrightarrow{MN}$|为( )| A. | $\frac{\sqrt{15}}{6}$ | B. | $\frac{\sqrt{6}}{6}$ | C. | $\frac{\sqrt{21}}{6}$ | D. | $\frac{\sqrt{15}}{3}$ |
分析 以AB,AD,AA1,分别为x,y,z轴,建立空间直角坐标系,确定向量 $\overrightarrow{AM}$、$\overrightarrow{AN}$的坐标,可得 $\overrightarrow{MN}$的坐标,从而可得|$\overrightarrow{MN}$|.
解答 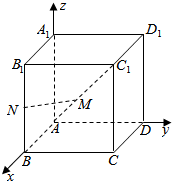 解:以AB,AD,AA1,分别为x,y,z轴,建立空间直角坐标系,则A(0,0,0),B(1,0,0),B1(1,0,1),C1(1,1,1)
解:以AB,AD,AA1,分别为x,y,z轴,建立空间直角坐标系,则A(0,0,0),B(1,0,0),B1(1,0,1),C1(1,1,1)
∴$\overrightarrow{{AC}_{1}}$=(1,1,1)
∵$\overrightarrow{AM}$=$\frac{1}{2}$$\overrightarrow{{AC}_{1}}$,∴$\overrightarrow{AM}$=($\frac{1}{3}$,$\frac{1}{3}$,$\frac{1}{3}$),
∵点N为B1B的中点,
∴$\overrightarrow{AN}$=(1,0,$\frac{1}{2}$)
∴$\overrightarrow{MN}$=($\frac{2}{3}$,-$\frac{1}{3}$,$\frac{1}{6}$)
∴|$\overrightarrow{MN}$|=$\sqrt{({\frac{2}{3})}^{2}+(-\frac{1}{3})^{2}+(\frac{1}{6})^{2}}$=$\frac{\sqrt{21}}{6}$
故选C.
点评 本题考查向量知识的运用,考查学生的计算能力,确定向量的坐标是关键.

练习册系列答案
相关题目
4.已知集合A={x∈R|log2x>0},B={x∈R|$\frac{x-2}{2x+1}$<0},则A∩B=( )
| A. | (0,2) | B. | (1,2) | C. | (-$\frac{1}{2}$,1) | D. | (2,+∞) |