题目内容
5．已知直线l：y=3x+3，那么直线x-y-2=0关于直线l对称的直线方程为7x+y+22=0．分析 在要求的直线上任意取一点M（x，y），设它关于直线l：y=3x+3的对称点为N（a，b），则点N在直线x-y-2=0上，即 a-b-2=0 ①．由垂直、和中点在对称轴上这两个条件求出a、b的解析式，再把a、b的解析式代入①，可得要求的直线方程．
解答 解：在直线x-y-2=0关于直线l对称的直线上任意取一点M（x，y），设它关于直线l：y=3x+3的对称点为N（a，b），
则点N在直线x-y-2=0上，即 a-b-2=0 ①．
由$\left\{\begin{array}{l}{\frac{b-y}{a-x}•3=-1}\\{\frac{b+y}{2}=3•\frac{a+x}{2}+3}\end{array}\right.$ 求得 $\left\{\begin{array}{l}{a=-\frac{4}{5}x+\frac{3}{5}y-\frac{9}{5}}\\{b=\frac{3}{5}x+\frac{4}{5}y+\frac{3}{5}}\end{array}\right.$ ②，
再把②代入①，可得7x+y+22=0，
故答案为：7x+y+22=0．
点评 本题主要考查求一个点关于某直线的对称点的坐标的方法，利用了垂直、和中点在对称轴上这两个条件，属于基础题．
练习册系列答案
相关题目
16．在满足条件$\left\{\begin{array}{l}{2x-y-2≤0}\\{3x+y-3≥0}\\{x+y-7≤0}\end{array}\right.$的区域内任取一点M（x，y），则点M（x，y）满足不等式（x-1）2+y2＜1的概率为（ ）
| A． | $\frac{π}{60}$ | B． | $\frac{π}{120}$ | C． | 1-$\frac{π}{60}$ | D． | 1-$\frac{π}{120}$ |
13．正方体ABCD-A1B1C1D1的棱长为1，点M在$\overline{A{C}_{1}}$上且$\overrightarrow{AM}$=$\frac{1}{2}$$\overrightarrow{M{C}_{1}}$，N为B1B的中点，则|$\overrightarrow{MN}$|为（ ）
| A． | $\frac{\sqrt{15}}{6}$ | B． | $\frac{\sqrt{6}}{6}$ | C． | $\frac{\sqrt{21}}{6}$ | D． | $\frac{\sqrt{15}}{3}$ |
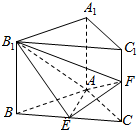如图，在直三棱柱ABC-A1B1C1中，△ABC为等腰直角三角形，∠BAC=90°，且AB=AA1，E、F分别为BC、CC1的中点．