题目内容
已知命题p关于x的方程x2+2ax+4=0无实数解;命题q:函数f(x)=(3-2a)x是增函数,若p∨q为真,p∧q为假,求实数a的取值范围.
设g(x)=x2+2ax+4,
由于关于x的方程x2+2ax+4=0无解
故△=4a2-16<0∴-2<a<2.
又因为f(x)=(3-2a)x是增函数,所以3-2a>0∴a<
又由于p∨q为真,p∧q为假,可知p和q一真一假
(1)若p真q假,则
,∴
≤a<2.
(2)若p假q真,则
∴a≤-2.
综上可知,实数a的取值范围为
≤a<2或a≤-2
由于关于x的方程x2+2ax+4=0无解
故△=4a2-16<0∴-2<a<2.
又因为f(x)=(3-2a)x是增函数,所以3-2a>0∴a<
| 3 |
| 2 |
又由于p∨q为真,p∧q为假,可知p和q一真一假
(1)若p真q假,则
|
| 3 |
| 2 |
(2)若p假q真,则
|
综上可知,实数a的取值范围为
| 3 |
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
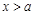 ,条件q:
,条件q: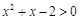 ,若p是q的充分不必要条件,则实数
,若p是q的充分不必要条件,则实数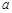 的取值范围是_____________.
的取值范围是_____________.