题目内容
(本题满分13分)已知二次函数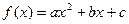 的图象经过点
的图象经过点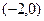 ,且不等式
,且不等式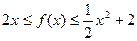 对一切实数
对一切实数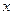 都成立.
都成立.
(1)求函数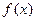 的解析式;
的解析式;
(2)若对一切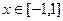 ,不等式
,不等式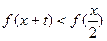 恒成立,求实数
恒成立,求实数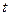 的取值范围.
的取值范围.
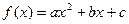 的图象经过点
的图象经过点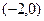 ,且不等式
,且不等式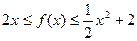 对一切实数
对一切实数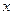 都成立.
都成立.(1)求函数
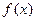 的解析式;
的解析式;(2)若对一切
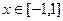 ,不等式
,不等式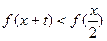 恒成立,求实数
恒成立,求实数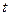 的取值范围.
的取值范围.解:(1)由题设知,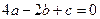 .
. 
 ①
①
令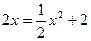 ,解得
,解得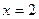 ,由题意可得
,由题意可得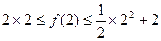 ,
,
即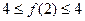 ,所以
,所以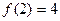 ,即
,即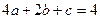 . ②
. ②
由①、②可得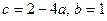 . …………………………………………………3分
. …………………………………………………3分
又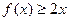 恒成立,即
恒成立,即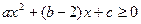 恒成立,
恒成立,
所以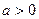 ,且
,且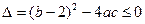
 ,
,
即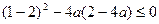 ,所以
,所以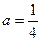 ,从而
,从而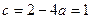 .
.
因此函数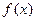 的解析式为
的解析式为 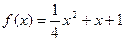 .…………………………………6分
.…………………………………6分
(2)由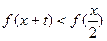 得
得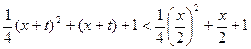 ,
,
整理得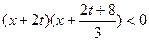 .
.
当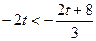 即
即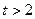 时,
时,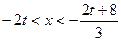 ,
,
此不等式对一切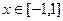 都成立的充要条件是
都成立的充要条件是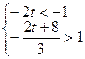 ,此不等式组无解.
,此不等式组无解.
当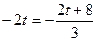 即
即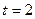 时,
时,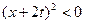 ,矛盾.
,矛盾.
当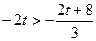 即
即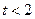 时,
时,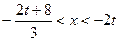 ,
,
此不等式对一切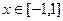 都成立的充要条件是
都成立的充要条件是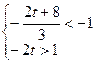 ,解得
,解得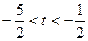 .
.
综合可知,实数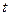 的取值范围是
的取值范围是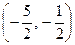 . ……………………………………13分
. ……………………………………13分
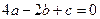 .
. 
 ①
①令
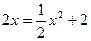 ,解得
,解得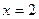 ,由题意可得
,由题意可得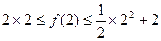 ,
,即
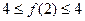 ,所以
,所以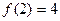 ,即
,即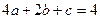 . ②
. ②由①、②可得
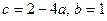 . …………………………………………………3分
. …………………………………………………3分又
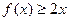 恒成立,即
恒成立,即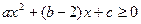 恒成立,
恒成立,所以
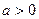 ,且
,且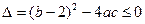
 ,
,即
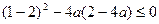 ,所以
,所以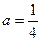 ,从而
,从而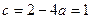 .
.因此函数
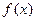 的解析式为
的解析式为 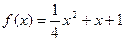 .…………………………………6分
.…………………………………6分(2)由
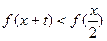 得
得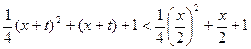 ,
,整理得
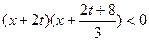 .
.当
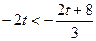 即
即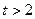 时,
时,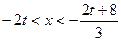 ,
,此不等式对一切
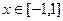 都成立的充要条件是
都成立的充要条件是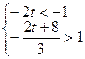 ,此不等式组无解.
,此不等式组无解.当
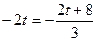 即
即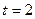 时,
时,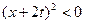 ,矛盾.
,矛盾.当
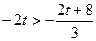 即
即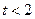 时,
时,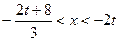 ,
,此不等式对一切
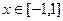 都成立的充要条件是
都成立的充要条件是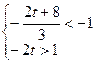 ,解得
,解得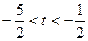 .
.综合可知,实数
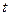 的取值范围是
的取值范围是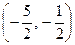 . ……………………………………13分
. ……………………………………13分略

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
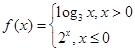 ,则
,则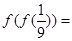 ( )
( )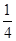
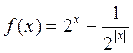
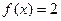 ,求
,求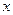 的值;
的值;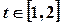 ,
,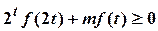 恒成立,求实数
恒成立,求实数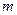 的取值范围。
的取值范围。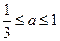 ,若函数
,若函数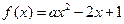 在区间
在区间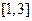 上
上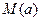 ,最小值为
,最小值为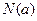 ,令
,令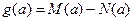 .
. 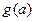 的函数表达式;
的函数表达式;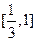 上的单调性,并求出
上的单调性,并求出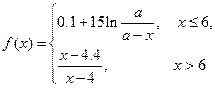
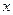 表示某学科知识的学习次数(
表示某学科知识的学习次数(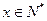 ),
),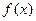 表示对该学科知识的掌握程度,正实数a与学科知识有关
表示对该学科知识的掌握程度,正实数a与学科知识有关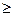 7时,掌握程度的增长量f(x+1)- f(x)总是下降;
7时,掌握程度的增长量f(x+1)- f(x)总是下降; 1,127]
1,127] 85%,请
85%,请 确定相应的学科.
确定相应的学科.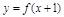 的图象如图1所示,它在定义域上是减函数,给出如下命题:①
的图象如图1所示,它在定义域上是减函数,给出如下命题:①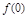 =1;②
=1;②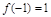 ;③若
;③若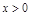 ,则
,则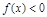 ;④若
;④若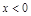 ,则
,则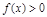 ,其中正确的是( )
,其中正确的是( )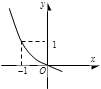
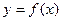
 与直线
与直线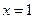 的交点个数为0或l;
的交点个数为0或l;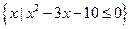 ,B={
,B={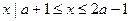 },若B
},若B 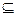 A,则-3
A,则-3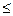 a
a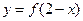 与函数
与函数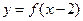 的图象关于直线
的图象关于直线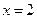 对称;
对称;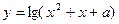 的值域为R的充要条件是:
的值域为R的充要条件是: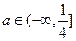 ;
;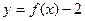 关于点(1,-1)对称的函数为
关于点(1,-1)对称的函数为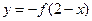 .
.