题目内容
(本小题满分14分)
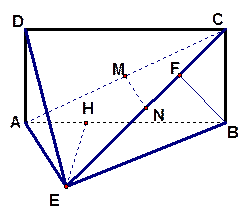
如图,四边形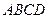 为矩形,
为矩形,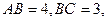 且
且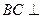 平面
平面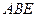 ,
,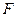 为
为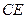 上的点,且
上的点,且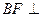 平面
平面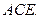
(1)设点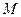 为线段
为线段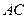 的中点,点
的中点,点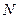 为线段
为线段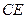 的中点,求证:
的中点,求证: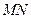 ∥平面
∥平面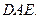

(2)求证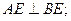

(3)当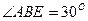 时,求三棱锥
时,求三棱锥 的体积。
的体积。
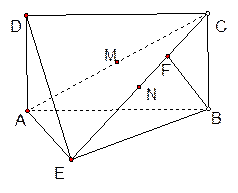
如图,四边形
 为矩形,
为矩形,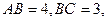 且
且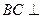 平面
平面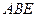 ,
,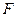 为
为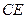 上的点,且
上的点,且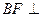 平面
平面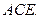
(1)设点
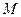 为线段
为线段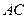 的中点,点
的中点,点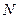 为线段
为线段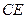 的中点,求证:
的中点,求证: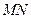 ∥平面
∥平面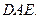

(2)求证
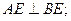

(3)当
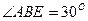 时,求三棱锥
时,求三棱锥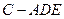 的体积。
的体积。
(本小题满分14分)
(1)∴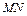 ∥平面
∥平面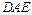 .
.
(2)∴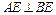
(3)∴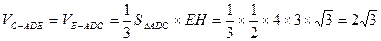
(1)∴
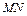 ∥平面
∥平面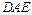 .
. (2)∴
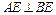
(3)∴
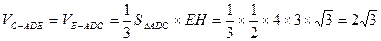
(本小题满分14分)
本题主要考查应用立体几何的基本知识进行直接推理和间接推理的能力.
证明:
(1)连接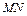 .
.
∵点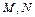 分别为线段
分别为线段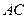 、
、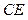 的中点,
的中点,
∴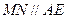 …………………………………………………………………2分
…………………………………………………………………2分
∵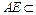 平面
平面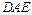 ,
,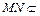 平面
平面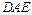 ,
,
∴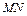 ∥平面
∥平面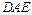 .…………………………………………………………4分
.…………………………………………………………4分
(2)∵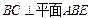 ,
,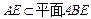 ,
,
∴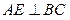 . ……………………………………………………………6分
. ……………………………………………………………6分
又∵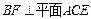 ,
,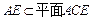 ,
,
∴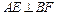 . …………………………………………………………………8分
. …………………………………………………………………8分
∵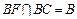 ,
,
∴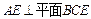 . …………………………………………………………9分
. …………………………………………………………9分
又∵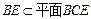 ,
,
∴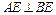 …………………………………………………………………10分
…………………………………………………………………10分
(3)过点E作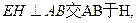 ………………………………………11分
………………………………………11分
由条件可知: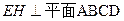 …………………………………………12分
…………………………………………12分
又由(1)知,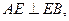 且
且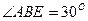 ,
,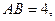
得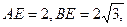 可求得
可求得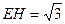 ………………………………13分
………………………………13分
∴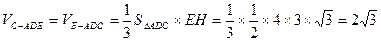 …………14分
…………14分
本题主要考查应用立体几何的基本知识进行直接推理和间接推理的能力.
证明:
(1)连接
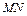 .
.∵点
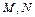 分别为线段
分别为线段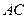 、
、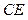 的中点,
的中点,∴
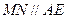 …………………………………………………………………2分
…………………………………………………………………2分∵
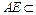 平面
平面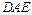 ,
,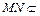 平面
平面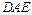 ,
,∴
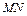 ∥平面
∥平面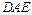 .…………………………………………………………4分
.…………………………………………………………4分 (2)∵
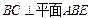 ,
,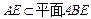 ,
,∴
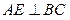 . ……………………………………………………………6分
. ……………………………………………………………6分又∵
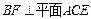 ,
,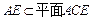 ,
,∴
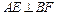 . …………………………………………………………………8分
. …………………………………………………………………8分∵
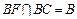 ,
, ∴
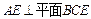 . …………………………………………………………9分
. …………………………………………………………9分又∵
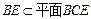 ,
,∴
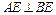 …………………………………………………………………10分
…………………………………………………………………10分(3)过点E作
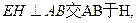 ………………………………………11分
………………………………………11分由条件可知:
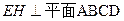 …………………………………………12分
…………………………………………12分又由(1)知,
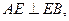 且
且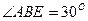 ,
,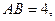
得
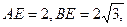 可求得
可求得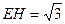 ………………………………13分
………………………………13分∴
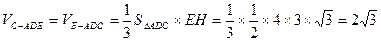 …………14分
…………14分

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
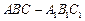 中,已知
中,已知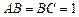 ,
,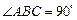 ,
,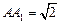 ,
,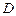 ,
,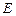 分别为
分别为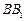 、
、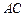 的中点.
的中点.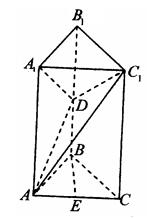
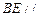 平面
平面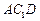 ;(II)求二面角
;(II)求二面角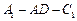 的大小.
的大小. 

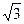 ,侧面PAD为等边三角形,并且与底面所成二面角为60
,侧面PAD为等边三角形,并且与底面所成二面角为60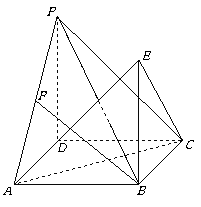
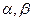 和两条不重合的直线
和两条不重合的直线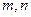 ,下列四个命题:
,下列四个命题: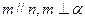 则
则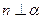 ②若
②若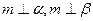 则
则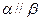
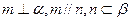 则
则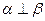 ④若
④若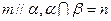 则
则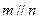
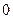 个
个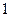 个
个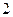 个
个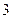 个
个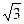 求二面角B-DC-A的正弦值。
求二面角B-DC-A的正弦值。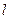 ,
,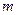 是两条不同的直线,
是两条不同的直线, 是一个平面,则下列命题正确的是
是一个平面,则下列命题正确的是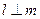 ,
,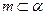 ,则
,则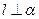
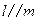 ,则
,则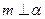
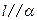 ,
,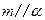 ,则
,则