题目内容

( 本小题满分12分)
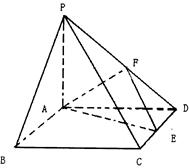
(普通中学做)如图,四棱锥P—ABCD中,底面ABCD 为矩形,AB=8,AD=4
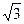 ,侧面PAD为等边三角形,并且与底面所成二面角为60
,侧面PAD为等边三角形,并且与底面所成二面角为60求PA与底面ABCD所成角的大小.
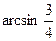
解:如图,取AD的中点E,连结PE,则PE⊥AD.
 作PO⊥平面ABCD,垂足为O,连结OE.
作PO⊥平面ABCD,垂足为O,连结OE.
根据三垂线定理的逆定理得OE⊥AD,
所以∠PEO为侧面PAD与底面所成的二面角的平面角--------6分
由已知条件可知∠PEO=60°,PE=6,
所以PO=3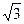 ,连结AO,则
,连结AO,则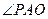 就是
就是
PA与底面ABCD所成角.在直角三角形POA中,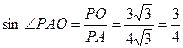
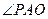 =
=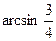 -------12分
-------12分
 作PO⊥平面ABCD,垂足为O,连结OE.
作PO⊥平面ABCD,垂足为O,连结OE.根据三垂线定理的逆定理得OE⊥AD,
所以∠PEO为侧面PAD与底面所成的二面角的平面角--------6分
由已知条件可知∠PEO=60°,PE=6,
所以PO=3
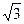 ,连结AO,则
,连结AO,则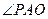 就是
就是PA与底面ABCD所成角.在直角三角形POA中,
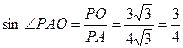
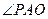 =
=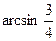 -------12分
-------12分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
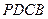 中,
中,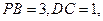
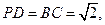
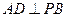
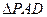 沿
沿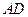 折起,使平面
折起,使平面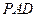 ⊥平面
⊥平面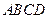 .
.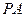 ⊥平面
⊥平面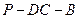 的大小;
的大小;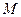 是侧棱
是侧棱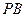 中点,求直线
中点,求直线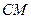 与平面
与平面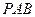 所成角的正弦值.
所成角的正弦值.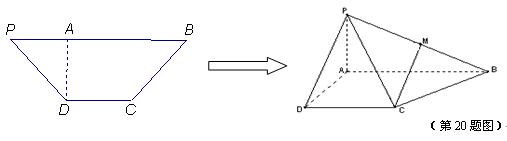
 与曲线
与曲线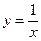 相切,分别求
相切,分别求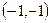 ;(2)
;(2)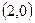 ;(3)
;(3)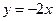 ;
;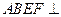 平面
平面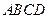 ,四边形
,四边形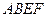 与
与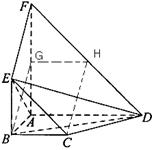
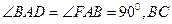
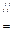
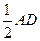 ,
,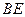
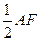 ,
,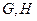 分别为
分别为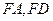 的中点
的中点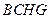 是平行四边形;
是平行四边形;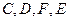 四点是否共面?为什么?
四点是否共面?为什么?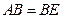 ,证明:平面
,证明:平面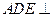 平面
平面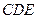 ;
;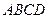 为矩形,
为矩形,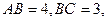 且
且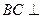 平面
平面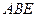 ,
,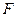 为
为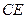 上的点,且
上的点,且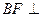 平面
平面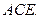
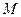 为线段
为线段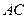 的中点,点
的中点,点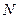 为线段
为线段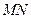 ∥平面
∥平面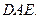

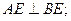
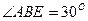 时,求三棱锥
时,求三棱锥 的体积。
的体积。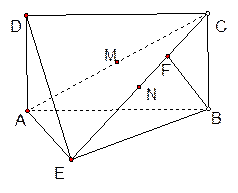
 的底面为正方形,
的底面为正方形,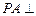 平面
平面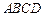 ,且
,且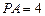 ,
,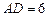 ,
,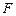 ,
,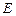 分别是线段
分别是线段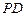 ,
,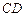 的中点.
的中点.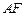 和
和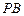 所成角的余弦值;
所成角的余弦值;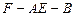 平面角的余弦值.
平面角的余弦值.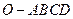 中,底面
中,底面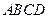 四边长为1的菱形,
四边长为1的菱形,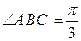 ,
,  ,
, 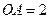 ,
,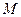 为
为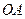 的中点,
的中点,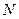 为
为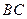 的中点,求异面直线OC与MN所成角的余弦值。
的中点,求异面直线OC与MN所成角的余弦值。
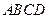 和
和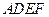 所在平面互相垂直,设
所在平面互相垂直,设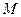 、
、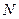 分别是
分别是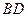 和
和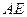 的中点,那么①
的中点,那么① 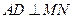 ;②
;② 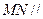 面
面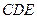 ;③
;③ 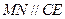 ;④
;④ 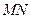 、
、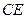 异面
异面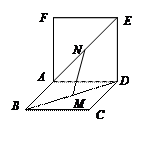
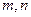 是两条不同的直线,
是两条不同的直线,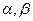 是两个不重合的平面,
是两个不重合的平面,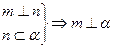 ;②
;②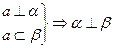
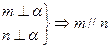 ;④
;④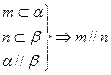
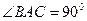 ,
,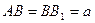 ,直线B1C与平面ABC成30°角。
,直线B1C与平面ABC成30°角。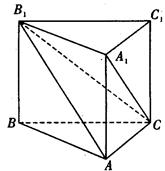
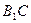 —A的正切值。
—A的正切值。