题目内容
在四面体ABCD中,DA⊥面ABC,∠ABC=90°,AE⊥CD,AF⊥DB.求证:
(1)EF⊥DC; (2)平面DBC⊥平面AEF; (3)若AD=AB=a,AC=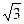 求二面角B-DC-A的正弦值。
求二面角B-DC-A的正弦值。
(1)EF⊥DC; (2)平面DBC⊥平面AEF; (3)若AD=AB=a,AC=
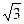 求二面角B-DC-A的正弦值。
求二面角B-DC-A的正弦值。略

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案
相关题目
题目内容
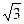 求二面角B-DC-A的正弦值。
求二面角B-DC-A的正弦值。
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案