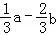题目内容
(2011•山东)设A1,A2,A3,A4是平面直角坐标系中两两不同的四点,若 (λ∈R),
(λ∈R), (μ∈R),且
(μ∈R),且 ,则称A3,A4调和分割A1,A2,已知点C(c,0),D(d,O)(c,d∈R)调和分割点A(0,0),B(1,0),则下面说法正确的是( )
,则称A3,A4调和分割A1,A2,已知点C(c,0),D(d,O)(c,d∈R)调和分割点A(0,0),B(1,0),则下面说法正确的是( )
 (λ∈R),
(λ∈R), (μ∈R),且
(μ∈R),且 ,则称A3,A4调和分割A1,A2,已知点C(c,0),D(d,O)(c,d∈R)调和分割点A(0,0),B(1,0),则下面说法正确的是( )
,则称A3,A4调和分割A1,A2,已知点C(c,0),D(d,O)(c,d∈R)调和分割点A(0,0),B(1,0),则下面说法正确的是( )| A.C可能是线段AB的中点 |
| B.D可能是线段AB的中点 |
| C.C,D可能同时在线段AB上 |
| D.C,D不可能同时在线段AB的延长线上 |
D
由已知可得(c,0)=λ(1,0),(d,0)=μ(1,0),
所以λ=c,μ=d,代入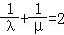 得
得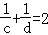 (1)
(1)
若C是线段AB的中点,则c=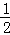 ,代入(1)d不存在,故C不可能是线段AB的中,A错误;同理B错误;
,代入(1)d不存在,故C不可能是线段AB的中,A错误;同理B错误;
若C,D同时在线段AB上,则0≤c≤1,0≤d≤1,代入(1)得c=d=1,此时C和D点重合,与条件矛盾,故C错误.
故选D
所以λ=c,μ=d,代入
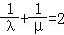 得
得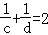 (1)
(1)若C是线段AB的中点,则c=
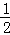 ,代入(1)d不存在,故C不可能是线段AB的中,A错误;同理B错误;
,代入(1)d不存在,故C不可能是线段AB的中,A错误;同理B错误;若C,D同时在线段AB上,则0≤c≤1,0≤d≤1,代入(1)得c=d=1,此时C和D点重合,与条件矛盾,故C错误.
故选D

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 为
为 所在平面上的一点,且
所在平面上的一点,且 ,其中
,其中 为实数,若点
为实数,若点



 中,
中,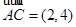 ,
,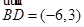 ,则该四边形的面积为( ).
,则该四边形的面积为( ). 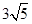
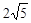
 对应的复数为1+2i,向量
对应的复数为1+2i,向量 对应的复数为3-i.
对应的复数为3-i.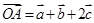 ,
,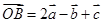 ,
,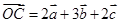 ,
,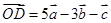 ,其中
,其中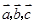 三向量不共面.试判断A,B,C,D四点是否共面?
三向量不共面.试判断A,B,C,D四点是否共面?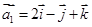 ,
,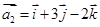 ,
,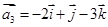 ,
,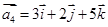 .试问是否存在实数
.试问是否存在实数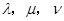 ,使
,使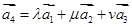 成立?如果存在,求出
成立?如果存在,求出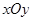 中,
中,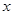 轴方向水平向右,
轴方向水平向右,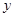 方向指向左上方,且
方向指向左上方,且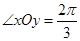 ,平面上任一点
,平面上任一点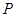 关于斜坐标系的斜坐标是这样定义的:若
关于斜坐标系的斜坐标是这样定义的:若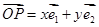 (其中向量
(其中向量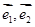 分别是与
分别是与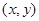 ,那么以
,那么以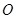 为顶点,
为顶点,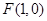 为焦点,
为焦点,


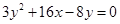
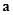 、
、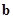 满足
满足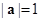 ,
,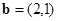 ,且
,且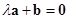 (
(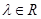 ),则
),则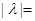 .
.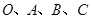 ,若
,若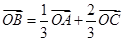 ,则
,则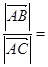 .
.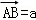 ,
,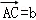 ,则
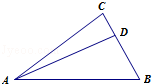
,则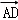 =( )
=( )
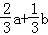 B.
B.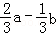 C.
C.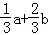 D.
D.