题目内容
已知复平面内平行四边形ABCD(A,B,C,D按逆时针排列),A点对应的复数为2+i,向量 对应的复数为1+2i,向量
对应的复数为1+2i,向量 对应的复数为3-i.
对应的复数为3-i.
(1)求点C,D对应的复数.
(2)求平行四边形ABCD的面积.
 对应的复数为1+2i,向量
对应的复数为1+2i,向量 对应的复数为3-i.
对应的复数为3-i.(1)求点C,D对应的复数.
(2)求平行四边形ABCD的面积.
(1)4-2i 5
(2)7
(2)7
(1)设点O为原点,因为向量 对应的复数为1+2i,向量
对应的复数为1+2i,向量 对应的复数为3-i,
对应的复数为3-i,
所以向量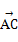 对应的复数为(3-i)-(1+2i)=2-3i,
对应的复数为(3-i)-(1+2i)=2-3i,
又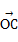 =
=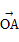 +
+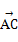 ,
,
所以点C对应的复数为(2+i)+(2-3i)=4-2i.
又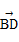 =
= +
+ =(1+2i)+(3-i)=4+i,
=(1+2i)+(3-i)=4+i,
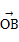 =
=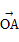 -
- =2+i-(1+2i)=1-i,
=2+i-(1+2i)=1-i,
所以 =
=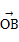 +
+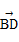 =1-i+(4+i)=5,
=1-i+(4+i)=5,
所以点D对应的复数为5.
(2)由(1)知 =(1,2),
=(1,2), =(3,-1),
=(3,-1),
因为 ·
· =|
=| ||
|| |cosB,
|cosB,
所以cosB=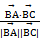 =
=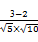 =
=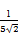 ,
,
所以sinB= ,
,
又| |=
|=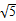 ,|
,| |=
|=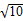 ,
,
所以面积S=| ||
|| |sinB=
|sinB=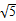 ×
×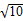 ×
× =7.
=7.
所以平行四边形ABCD的面积为7.
 对应的复数为1+2i,向量
对应的复数为1+2i,向量 对应的复数为3-i,
对应的复数为3-i,所以向量
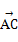 对应的复数为(3-i)-(1+2i)=2-3i,
对应的复数为(3-i)-(1+2i)=2-3i,又
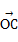 =
=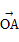 +
+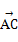 ,
,所以点C对应的复数为(2+i)+(2-3i)=4-2i.
又
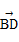 =
= +
+ =(1+2i)+(3-i)=4+i,
=(1+2i)+(3-i)=4+i,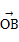 =
=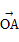 -
- =2+i-(1+2i)=1-i,
=2+i-(1+2i)=1-i,所以
 =
=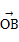 +
+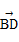 =1-i+(4+i)=5,
=1-i+(4+i)=5,所以点D对应的复数为5.
(2)由(1)知
 =(1,2),
=(1,2), =(3,-1),
=(3,-1),因为
 ·
· =|
=| ||
|| |cosB,
|cosB,所以cosB=
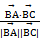 =
=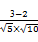 =
=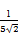 ,
,所以sinB=
 ,
,又|
 |=
|=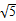 ,|
,| |=
|=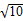 ,
,所以面积S=|
 ||
|| |sinB=
|sinB=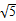 ×
×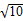 ×
× =7.
=7.所以平行四边形ABCD的面积为7.

练习册系列答案
相关题目
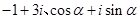 (
(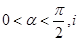 是虚数单位)在复平面上对应的点依次为
是虚数单位)在复平面上对应的点依次为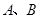 ,点
,点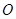 是坐标原点.
是坐标原点.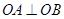 ,求
,求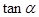 的值;
的值; 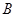 点的横坐标为
点的横坐标为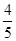 ,求
,求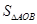 .
.
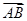 =
=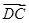 =(1,1),
=(1,1),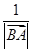 ·
·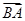 +
+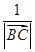 ·
·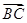 =
=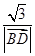 ·
·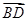 ,则四边形ABCD的面积为________.
,则四边形ABCD的面积为________.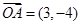 ,
,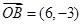 ,
,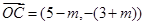 .
.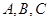 能构成三角形,求实数
能构成三角形,求实数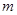 应满足的条件;
应满足的条件;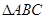 为直角三角形,且
为直角三角形,且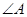 为直角,求实数
为直角,求实数 (λ∈R),
(λ∈R), (μ∈R),且
(μ∈R),且 ,则称A3,A4调和分割A1,A2,已知点C(c,0),D(d,O)(c,d∈R)调和分割点A(0,0),B(1,0),则下面说法正确的是( )
,则称A3,A4调和分割A1,A2,已知点C(c,0),D(d,O)(c,d∈R)调和分割点A(0,0),B(1,0),则下面说法正确的是( )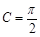 ,
,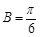 ,
,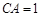 ,则
,则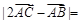 _____.
_____. ,若a=e1+3e2,b=2e1,则向量a在b方向上的射影为________.
,若a=e1+3e2,b=2e1,则向量a在b方向上的射影为________.