题目内容
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数).在以坐标原点
为参数).在以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴建立的极坐标系中,曲线
轴正半轴为极轴建立的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
(1)求直线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 分别相交于异于原点的点
分别相交于异于原点的点![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1) 直线![]() 的极坐标方程为:
的极坐标方程为:![]() .
.![]() 的直角坐标方程为
的直角坐标方程为![]() . (2)
. (2) ![]()
【解析】
(1)由直线的参数方程可知,直线过原点且倾斜角直线![]() 的为
的为![]() 的直线,由此可表示出直线的极坐标;利用极坐标与直角坐标的互化公式即可得到曲线
的直线,由此可表示出直线的极坐标;利用极坐标与直角坐标的互化公式即可得到曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)点![]() 的极坐标分别为
的极坐标分别为![]() ,得到|PQ| ,再利用三角函数的性质求出
,得到|PQ| ,再利用三角函数的性质求出![]() 的取值范围。
的取值范围。
解:(1)因为直线![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数),
为参数),
所以直线![]() 表示过原点且倾斜角直线
表示过原点且倾斜角直线![]() 的为
的为![]() 的直线,则其极坐标方程为:
的直线,则其极坐标方程为:
![]() .
.
曲线![]() 的极坐标方程
的极坐标方程![]() 可化为
可化为![]() ,
,
即![]() ,
,
因此曲线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
(2)设点![]() 的极坐标分别为
的极坐标分别为![]() ,
,
则
![]()
因为![]() ,即
,即![]() ,所以
,所以![]() 的取值范围为
的取值范围为![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】《山东省高考改革试点方案》规定:从![]() 年高考开始,高考物理、化学等六门选考科目的考生原始成绩从高到低划分为
年高考开始,高考物理、化学等六门选考科目的考生原始成绩从高到低划分为![]() 八个等级.参照正态分布原则,确定各等级人数所占比例分别为
八个等级.参照正态分布原则,确定各等级人数所占比例分别为![]() .选考科目成绩计入考生总成绩时,将
.选考科目成绩计入考生总成绩时,将![]() 至
至![]() 等级内的考生原始成绩,依照等比例转换法则分别转换到
等级内的考生原始成绩,依照等比例转换法则分别转换到![]()
![]() 八个分数区间,得到考生的等级成绩.
八个分数区间,得到考生的等级成绩.
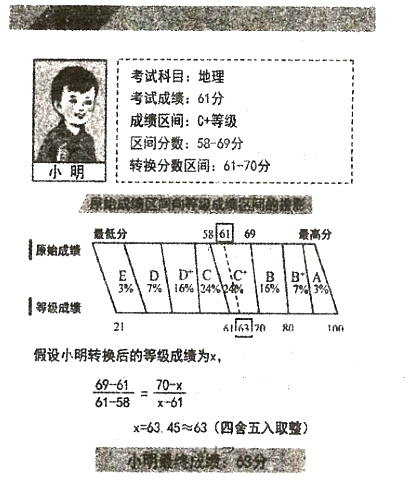
某校![]() 级学生共
级学生共![]() 人,以期末考试成绩为原始成绩转换了本校的等级成绩,为学生合理选科提供依据,其中物理成绩获得等级
人,以期末考试成绩为原始成绩转换了本校的等级成绩,为学生合理选科提供依据,其中物理成绩获得等级![]() 的学生原始成绩统计如下
的学生原始成绩统计如下
成绩 | 93 | 91 | 90 | 88 | 87 | 86 | 85 | 84 | 83 | 82 |
人数 | 1 | 1 | 4 | 2 | 4 | 3 | 3 | 3 | 2 | 7 |
(1)从物理成绩获得等级![]() 的学生中任取
的学生中任取![]() 名,求恰好有
名,求恰好有![]() 名同学的等级分数不小于
名同学的等级分数不小于![]() 的概率;
的概率;
(2)待到本级学生高考结束后,从全省考生中不放回的随机抽取学生,直到抽到![]() 名同学的物理高考成绩等级为
名同学的物理高考成绩等级为![]() 或
或![]() 结束(最多抽取
结束(最多抽取![]() 人),设抽取的学生个数为
人),设抽取的学生个数为![]() ,求随机变量
,求随机变量![]() 的数学期望(注:
的数学期望(注: ![]() ).
).