题目内容
【题目】过抛物线
的焦点
作直线交抛物线于
两点，已知点
，
为坐标原点.若
的最小值为3.
(1)求抛物线的方程；
(2)过点作直线
，交抛物线于
两点，求
的取值范围.
【答案】（1）
，（2）
【解析】
（1）利用抛物线的定义，通过数形结合分析得到最小值即为点M到准线的距离
解方程即得抛物线的方程；（2）可设直线AB方程为
，求出
，
，再利用基本不等式得解.
（1）
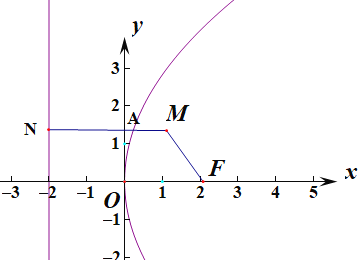
由题得点
是抛物线的准线，
因为A是抛物线上的动点，由抛物线的定义可知，|AF|=
（动点A到准线的距离），
又p>2,所以当x=1时，
，所以定点M（1,2）在抛物线的内部，
过点M作准线的垂线，垂足为N,交抛物线于点
点，
当动点A取点时，|AF|+|AM|此时最小，最小值即为点M到准线的距离
.
（2）由题得此时直线AB的斜率存在，可设直线AB方程为，
直线CD方程为：
，
把直线AB的方程和抛物线的方程联立得：
设
所以
，
同理可得
所以原式=
，
当且仅当
时取等，所以
的取值范围为.
【题目】如图，四棱锥
的底面是菱形，
底面
，
分别是
的中点，
，
，
.
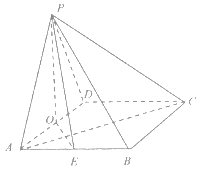
（I）证明：
；
（II）求直线
与平面
所成角的正弦值；
（III）在
边上是否存在点
，使
与
所成角的余弦值为
，若存在，确定点位置；若不存在，说明理由.
【题目】运动健康已成为大家越来越关心的话题，某公司开发的一个类似计步数据库的公众号．手机用户可以通过关注该公众号查看自己每天行走的步数，同时也可以和好友进行运动量的PK和点赞．现从张华的好友中随机选取40人（男、女各20人），记录他们某一天行走的步数，并将数据整理如表：
步数 性别 | 0～2000 | 2001～5000 | 5001～8000 | 8001～10000 | ＞10000 |
男 | 1 | 2 | 4 | 7 | 6 |
女 | 0 | 3 | 9 | 6 | 2 |
（1）若某人一天行走的步数超过8000步被评定为“积极型”，否则被评定为“懈怠型”，根据题意完成下列2×2列联表，并据此判断能否有90%的把握认为男、女的“评定类型”有差异？
积极型 | 懈怠型 | 总计 | |
男 | |||
女 | |||
总计 |
（2）在张华的这40位好友中，从该天行走的步数不超过5000步的人中随机抽取2人，设抽取的女性有X人，求X=1时的概率．
参考公式与数据：
P（K2≥k0） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
K2=
，其中n=a+b+c+d．