题目内容
已知关于x的方程x2-3x+a=0和x2-3x+b=0(a≠b)的四个根组成首项为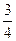 的等差数列,求a+b的值.
的等差数列,求a+b的值.
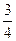 的等差数列,求a+b的值.
的等差数列,求a+b的值.a+b=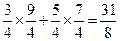
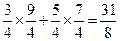
由方程x2-3x+a=0和x2-3x+b=0(a≠b)可设两方程的根分别为x1,x2和x3,x4,
由x1+x2=3和x3+x4=3
所以,x1,x3,x4,x2(或x3,x1,x2,x4)组成等差数列,
由首项x1=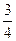 ,x1+x3+x4+x2=6,可求公差d=
,x1+x3+x4+x2=6,可求公差d=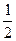 ,
,
所以四项为: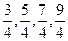 ,
,
∴a+b=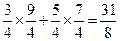
由x1+x2=3和x3+x4=3
所以,x1,x3,x4,x2(或x3,x1,x2,x4)组成等差数列,
由首项x1=
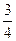 ,x1+x3+x4+x2=6,可求公差d=
,x1+x3+x4+x2=6,可求公差d=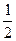 ,
,所以四项为:
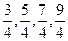 ,
,∴a+b=
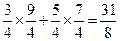

练习册系列答案
相关题目
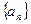 满足
满足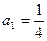 ,
,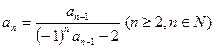 .
.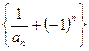 是否为等比数列,并说明理由;
是否为等比数列,并说明理由;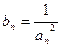 ,求数列
,求数列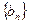 的前
的前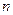 项和
项和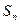 ;(3)设
;(3)设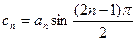 ,数列
,数列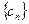 的前
的前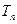 .求证:对任意的
.求证:对任意的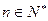 ,
,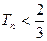 .
.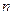 为正整数时,区间
为正整数时,区间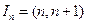 ,
,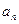 表示函数
表示函数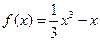 在
在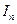 上函数值取整数值的个数,当
上函数值取整数值的个数,当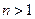 时,记
时,记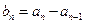 .当
.当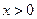 ,
,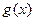 表示把
表示把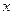 “四舍五入”到个位的近似值,如
“四舍五入”到个位的近似值,如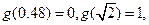
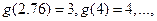 当
当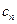 表示满足
表示满足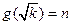 的正整数
的正整数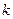 的个数.
的个数.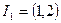 的单调性;
的单调性;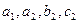 ;
;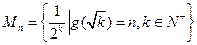 中所有元素之和为
中所有元素之和为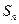 ,记
,记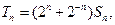 求证:
求证: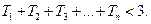
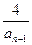 (n≥2),令bn=
(n≥2),令bn=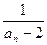 .
.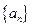 满足递推关系
满足递推关系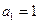 且
且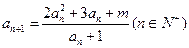 .
.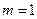 时,求数列
时,求数列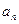 ;(2) 当
;(2) 当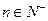 时,数列
时,数列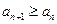 恒成立,求
恒成立,求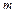 的取值范围;(3) 在
的取值范围;(3) 在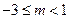 时,证明:
时,证明: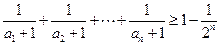 .
.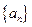 中,a1=8,a4=2且满足an+2=2an+1-an,(n∈N*)
中,a1=8,a4=2且满足an+2=2an+1-an,(n∈N*)
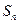 =|a1|+|a2|+…+|an|,求
=|a1|+|a2|+…+|an|,求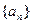 是等差数列,
是等差数列,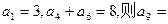 .
.