题目内容
已知数列{an}满足a1=4,an=4-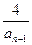 (n≥2),令bn=
(n≥2),令bn=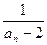 .
.
(1)求证数列{bn}是等差数列;
(2)求数列{an}的通项公式.
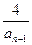 (n≥2),令bn=
(n≥2),令bn=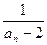 .
.(1)求证数列{bn}是等差数列;
(2)求数列{an}的通项公式.
(1)同解析,(2)数列{an}的通项公式an=2+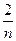
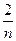
.(1)证明:an+1-2=2-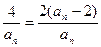
∴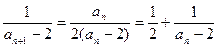 (n≥1)
(n≥1)
故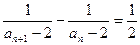 (n≥1),即bn+1-bn=
(n≥1),即bn+1-bn=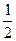 (n≥1)
(n≥1)
∴数列{bn}是等差数列.
(2)解析:∵{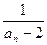 }是等差数列
}是等差数列
∴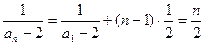 , ∴an=2+
, ∴an=2+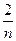
∴数列{an}的通项公式an=2+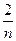
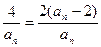
∴
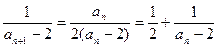 (n≥1)
(n≥1)故
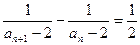 (n≥1),即bn+1-bn=
(n≥1),即bn+1-bn=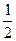 (n≥1)
(n≥1)∴数列{bn}是等差数列.
(2)解析:∵{
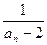 }是等差数列
}是等差数列∴
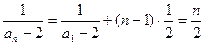 , ∴an=2+
, ∴an=2+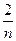
∴数列{an}的通项公式an=2+
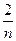

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
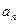 }的前n项和为
}的前n项和为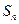 ,已知对任意的
,已知对任意的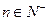 ,点
,点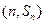 ,均在函数
,均在函数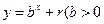 且
且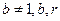 均为常数)的图像上。
均为常数)的图像上。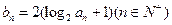 ,证明:对任意的
,证明:对任意的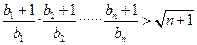 成立。
成立。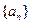 中,
中,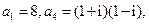 且满足
且满足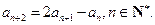
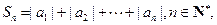 求
求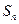 的解析式;
的解析式;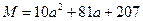 ,
,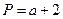 ,Q=
,Q=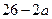 ;若将
;若将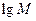 ,
,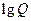 ,
,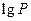 适当排序后可构成公差为1的等差数列
适当排序后可构成公差为1的等差数列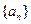 的前三项
的前三项 (I)在使得
(I)在使得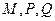 的大小;
的大小;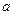 的值及数列
的值及数列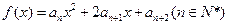 的图象在
的图象在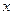 轴上截得的线段长为
轴上截得的线段长为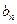 ,设
,设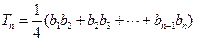 ,求
,求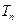 .
.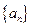 满足
满足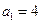 ,点
,点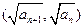 在直线
在直线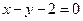 上,
上,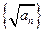 是等差数列;(2)求数列
是等差数列;(2)求数列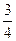 的等差数列,求a+b的值.
的等差数列,求a+b的值.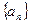 中,a1=1,前
中,a1=1,前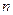 项和为
项和为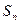 ,
,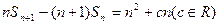 且
且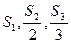 成等差数列。
成等差数列。 的值; (2)求数列
的值; (2)求数列