题目内容
已知数列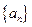 中,a1=8,a4=2且满足an+2=2an+1-an,(n∈N*)
中,a1=8,a4=2且满足an+2=2an+1-an,(n∈N*)
(1)求数列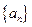 的通项公式;(2)设
的通项公式;(2)设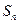 =|a1|+|a2|+…+|an|,求
=|a1|+|a2|+…+|an|,求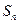 .
.
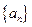 中,a1=8,a4=2且满足an+2=2an+1-an,(n∈N*)
中,a1=8,a4=2且满足an+2=2an+1-an,(n∈N*)
(1)求数列
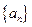 的通项公式;(2)设
的通项公式;(2)设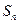 =|a1|+|a2|+…+|an|,求
=|a1|+|a2|+…+|an|,求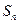 .
.(1)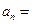 10-2n;(2)
10-2n;(2) 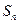 =
=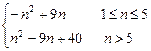
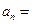 10-2n;(2)
10-2n;(2) 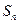 =
=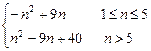
(1)由an+2=2an+1-an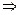 an+2-an+1=an+1-an可知
an+2-an+1=an+1-an可知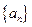 成等差数列,
成等差数列,
∴公差d=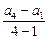 =-2,∴数列
=-2,∴数列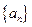 的通项公式为
的通项公式为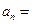 10-2n
10-2n .
.
(2)由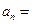 10-2n≥0可得n≤5,∴当n≤5时,
10-2n≥0可得n≤5,∴当n≤5时,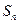 =-n2+9n;当n>5时,
=-n2+9n;当n>5时,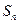 =n2-9n+40,
=n2-9n+40,
所以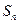 =
=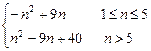 .
.
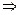 an+2-an+1=an+1-an可知
an+2-an+1=an+1-an可知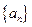 成等差数列,
成等差数列,∴公差d=
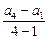 =-2,∴数列
=-2,∴数列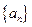 的通项公式为
的通项公式为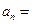 10-2n
10-2n .
.(2)由
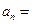 10-2n≥0可得n≤5,∴当n≤5时,
10-2n≥0可得n≤5,∴当n≤5时,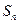 =-n2+9n;当n>5时,
=-n2+9n;当n>5时,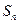 =n2-9n+40,
=n2-9n+40,所以
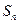 =
=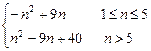 .
.
练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
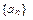 满足
满足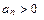 ,且对一切
,且对一切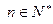 有
有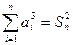 ,其中
,其中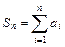 ,
, 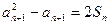 ,并求数列
,并求数列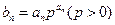 ,求数列
,求数列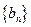 的前
的前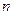 项和
项和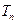 ;
;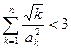 .
. 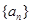 是等差数列,首项
是等差数列,首项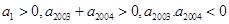 ,则使前n项和
,则使前n项和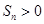 成立的最大自然数n是:
成立的最大自然数n是: 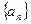 的公比为
的公比为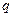 ,前n项和为
,前n项和为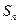 ,若
,若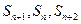 成等差数列,则
成等差数列,则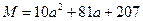 ,
,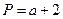 ,Q=
,Q=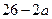 ;若将
;若将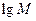 ,
,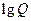 ,
,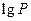 适当排序后可构成公差为1的等差数列
适当排序后可构成公差为1的等差数列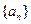 的前三项
的前三项 (I)在使得
(I)在使得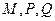 的大小;
的大小;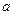 的值及数列
的值及数列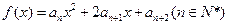 的图象在
的图象在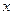 轴上截得的线段长为
轴上截得的线段长为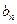 ,设
,设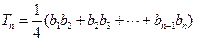 ,求
,求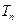 .
.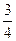 的等差数列,求a+b的值.
的等差数列,求a+b的值.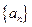 满足
满足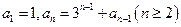 ,试写出
,试写出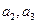 , 并求数列
, 并求数列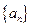 中,
中,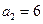 ,
,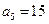 ,若
,若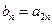 ,则数列
,则数列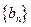 的前5项和等于( )
的前5项和等于( )