题目内容
14.已知点A(-2,0),B(0,4),点P在圆C:(x-3)2+(y-4)2=5上,则使∠APB=90°的点P的个数为( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 设P(x,y),要使∠APB=90°,只要求出P到AB中点的距离以及圆上的所有点到AB中点距离范围.
解答 解:设P(x,y),要使∠APB=90°,那么P到AB中点(-1,2)的距离为$\sqrt{(x+1)^{2}+(y-2)^{2}}=\frac{1}{2}AB=\sqrt{5}$,
而圆上的所有点到AB中点距离范围为[$\sqrt{(3+1)^{2}+(4-2)^{2}}-\sqrt{5}$,$\sqrt{(3+1)^{2}+(4-2)^{2}}+\sqrt{5}$],即[$\sqrt{5}$,3$\sqrt{5}$],
所以使∠APB=90°的点P的个数只有一个,就是AB中点与圆心连线与圆的交点;
故选B
点评 本题考查了点与圆的位置关系的判断;关键是明确线段AB中点与圆上点的距离范围.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.运行如图所示的程度框图,若输出结果为$\frac{4029}{2015}$,则判断框中应该填的条件是( )
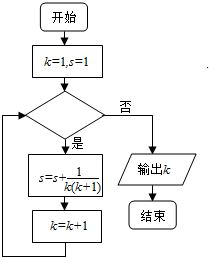

| A. | k<2012 | B. | k<2013 | C. | k<2014 | D. | k<2015 |
2.若向量$\overrightarrow{a}$•$\overrightarrow{b}$=-2,|$\overrightarrow{a}$|=4,|$\overrightarrow{b}$|=1,则向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为( )
| A. | $\frac{2π}{3}$ | B. | $\frac{π}{3}$ | C. | $\frac{5π}{6}$ | D. | $\frac{π}{6}$ |
9.在△ABC中,BC=6,若G,O分别为△ABC的重心和外心,且$\overrightarrow{OG}$•$\overrightarrow{BC}$=6,则△ABC的形状是( )
| A. | 锐角三角形 | B. | 钝角三角形 | ||
| C. | 直角三角形 | D. | 上述三种情况都有可能 |
3.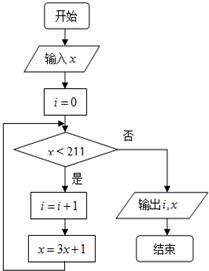 运行如图所示的程序流程图.
运行如图所示的程序流程图.
(1)若输入x的值为2,根据该程序的运行过程填写下面的表格,并求输出i与x的值;
(2)从问题(1)表格中填写的x的5个数值中任取两个数,求这两个数的平均数大于211的概率;
(3)若输出i的值为2,求输入x的取值范围.
 运行如图所示的程序流程图.
运行如图所示的程序流程图.(1)若输入x的值为2,根据该程序的运行过程填写下面的表格,并求输出i与x的值;
| 第i次 | i=1 | i=2 | i=3 | i=4 | i=5 |
| x= | 7 | 22 | 67 | 202 | 607 |
(3)若输出i的值为2,求输入x的取值范围.
4.等差数列{an}中,已知a1=2,a3+a5=10,则a7等于( )
| A. | 5 | B. | 6 | C. | 8 | D. | 10 |