题目内容
【题目】如图，四棱锥
中，
⊥平面
，底面为正方形，
为
的中点，
.
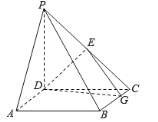
（1）求证：
；
（2）
边上是否存在一点
，使得
//平面
？若存在，求
的长，若不存在，请说明理由.
【答案】（1）见解析；（2）23.
【解析】分析：（1）要证明
，需证
面
，需证：
，用分析法书写即可。
（2）连结AC,取AC中点O,连结EO,GO,延长GO交AD于点M,则PA∥平面MEG，再求解
详解：(Ⅰ)证明：∵PD⊥平面A
CD，∴PD⊥BC
又∵ABCD是正方形∴BC⊥CD
∵PD∩CD=D
∴BC⊥平面PCD
又∵PC面PBC
∴PC⊥BC
（2）连结AC,取AC中点O,连结EO,GO,延长GO交AD于点M,则PA∥平面MEG
下面证明之
∵E为PC的中点，O是AC的中点，
∴EO∥PA,
又∵EO平面MEG，PA平面MEG
∴PA∥平面MEG
在正方形ABCD中,∵O是AC的中点,∴△OCG≌△OAM，
∴AM=CG=23,∴所求AM的长为23.
练习册系列答案
相关题目
