题目内容
【题目】如图1,已知直角梯形ABCD中,![]() ,AB//DC,AB⊥AD,E为CD的中点,沿AE把△DAE折起到△PAE的位置(D折后变为P),使得PB=2,如图2.
,AB//DC,AB⊥AD,E为CD的中点,沿AE把△DAE折起到△PAE的位置(D折后变为P),使得PB=2,如图2.
(Ⅰ)求证:平面PAE⊥平面ABCE;
(Ⅱ)求点B到平面PCE的距离.

【答案】(1)见解析(2)![]()
【解析】试题分析:![]() 取
取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,可知
,可知![]() ,
,![]() 为等腰直角三角形,证得
为等腰直角三角形,证得![]() ,
,![]() ,再由勾股定理证得
,再由勾股定理证得![]() ,即可证明
,即可证明 ![]() 利用等体积法
利用等体积法![]() ,即可求点
,即可求点![]() 到平面
到平面![]() 的距离
的距离
解析:(Ⅰ)如图,取AE的中点O,连接PO,OB,BE.由于在平面图形中,如题图1,连接BD,BE,易知四边形ABED为正方形, ∴在立体图形中,△PAE,△BAE为等腰直角三角形,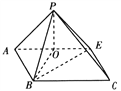
∴PO⊥AE,OB⊥AE,PO=OB=![]() ,
,
∵PB=2,∴![]() ,
,
∴PO⊥OB
又![]() ,∴平面PO⊥平面ABCE,
,∴平面PO⊥平面ABCE,
∵PO![]() 平面PAE,∴平面PAE⊥平面ABCD
平面PAE,∴平面PAE⊥平面ABCD
(Ⅱ)由(Ⅰ)可知,PO⊥AE,OB⊥AE,![]() ,故AE⊥平面POB.
,故AE⊥平面POB.
∵PB![]() 平面POB,∴AE⊥PB,又BC//AE,∴BC⊥PB.
平面POB,∴AE⊥PB,又BC//AE,∴BC⊥PB.
在Rt△PBC中,![]()
在△PEC中,PE=CE=2,
∴![]()
设点B到平面PCE的距离为d,由![]() ,
,
得![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

