题目内容
【题目】二进制规定：每个二进制数由若干个0、1组成，且最高位数字必须为1.若在二进制中，
是所有
位二进制数构成的集合，对于
，
，
表示和
对应位置上数字不同的位置个数.例如当
，
时
，当，
时
.
（1）令
，求所有满足
，且
的
的个数；
（2）给定
，对于集合中的所有，求的和.
【答案】（1）
；（2）
.
【解析】试题分析：
（1）由题意可知
为5位数且与
有2项不同，由排列组合公式可得的个数为.
（2）由题意可知
的和
，倒叙相加可得的和为
.
试题解析：
（1）因为
，所以为5位数且与有2项不同，
又因为首项为1，故与在后四项中有两项不同，所以的个数为.
（2）当=0时，
的个数为
；
当=1时，的个数为
，
当=2时，的个数为
，
………
当
时，的个数为
，
设的和为
， 则，
倒序得
，
倒序相加得
，即
，
所以的和为.
【题目】依据某地某条河流8月份的水文观测点的历史统计数据所绘制的频率分布直方图如图（甲）所示；依据当地的地质构造，得到水位与灾害等级的频率分布条形图如图（乙）所示．
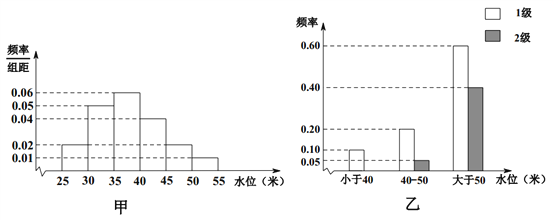
试估计该河流在8月份水位的中位数；
（1）以此频率作为概率，试估计该河流在8月份发生1级灾害的概率；
（2）该河流域某企业，在8月份，若没受1、2级灾害影响，利润为500万元；若受1级灾害影响，则亏损100万元；若受2级灾害影响则亏损1000万元．
现此企业有如下三种应对方案：
方案 | 防控等级 | 费用（单位：万元） |
方案一 | 无措施 | 0 |
方案二 | 防控1级灾害 | 40 |
方案三 | 防控2级灾害 | 100 |
试问，如仅从利润考虑，该企业应选择这三种方案中的哪种方案？说明理由．
【题目】据中国日报网报道：2017年11月13日，TOP500发布的最新一期全球超级计算机500强榜单显示，中国超算在前五名中占据两席，其中超算全球第一“神威太湖之光”完全使用了国产品牌处理器。为了了解国产品牌处理器打开文件的速度，某调查公司对两种国产品牌处理器进行了12次测试，结果如下（数值越小，速度越快，单位是MIPS）
测试1 | 测试2 | 测试3 | 测试4 | 测试5 | 测试6 | 测试7 | 测试8 | 测试9 | 测试10 | 测试11 | 测试12 | |
品牌A | 3 | 6 | 9 | 10 | 4 | 1 | 12 | 17 | 4 | 6 | 6 | 14 |
品牌B | 2 | 8 | 5 | 4 | 2 | 5 | 8 | 15 | 5 | 12 | 10 | 21 |
设
分别表示第次测试中品牌A和品牌B的测试结果，记
（Ⅰ）求数据
的众数；
（Ⅱ）从满足
的测试中随机抽取两次，求品牌A的测试结果恰好有一次大于品牌B的测试结果的概率；
（Ⅲ）经过了解，前6次测试是打开含有文字和表格的文件，后6次测试是打开含有文字和图片的文件.请你依据表中数据，运用所学的统计知识，对这两种国产品牌处理器打开文件的速度进行评价.
